Числа Фибоначчи
Числа Фибоначчи — числовая последовательность, первые два элемента которой равны 1, а каждый последующий равен сумме двух предыдущих.
Вывод программы должен выглядеть следующим образом: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, …
Отметим, что данный пример может быть реализован несколькими способами:
- непосредственно через рекурсивное определение: наименее эффективный способ, позволяющий в то же время продемонстрировать использование рекурсивных функций.
- с сохранением вычисленных чисел в массиве: более эффективный способ, позволяющий продемонстрировать работу с массивами.
- через формулу Бине: наиболее эффективный способ, позволяющий продемонстрировать работу с математическими функциями.
Пример для версий Free Pascal 2.2.0, Free Pascal 2.2.4, gpc 20070904, PascalABC.NET 1.8, Turbo Pascal 1.0, Turbo Pascal 2.0, Turbo Pascal 3.0, Turbo Pascal 4.0, Turbo Pascal 5.0, Turbo Pascal 5.5, Turbo Pascal 6.0, Turbo Pascal 7.0
Этот пример использует рекурсивное определение чисел Фибоначчи.
program fibonacci;
function fib(n:integer): integer;
begin
if (n <= 2) then
fib := 1
else
fib := fib(n-1) + fib(n-2);
end;
var
i:integer;
begin
for i := 1 to 16 do
write(fib(i), ', ');
writeln('...');
end.
Пример для версий Euphoria 3.1.1
function fib(integer n)
sequence f
if n = 1 then
return {1}
elsif n = 2 then
return {1,1}
else
f = fib(n-1)
f = append(f, f[$-1] + f[$])
return f
end if
end function
print(1,fib(16))
Пример для версий clisp 2.47, Corman Common Lisp 3.0, gcl 2.6.6, SBCL 1.0.1, SBCL 1.0.29
Используется рекурсивное определение чисел Фибоначчи. Часть finally макроса loop выполняется после конца цикла.
(defun fibonacci (n)
(if (< n 3)
1
(+ (fibonacci (- n 1)) (fibonacci (- n 2))) ))
(loop for i from 1 to 16
do (format t "~D, " (fibonacci i))
finally (format t "...~%"))
Пример для версий Borland C++ Builder 6, g++ 3.4.5, Microsoft Visual C++ 6, Microsoft Visual C++ 9 (2008)
#include <iostream>
int fibonacci(int n)
{
return (n<=2 ? 1 : fibonacci(n-1) + fibonacci(n-2));
}
int main(void)
{
for (int n=1; n<=16; n++)
std::cout << fibonacci(n) << ", ";
std::cout << "..." << std::endl;
return 0;
}
Пример для версий gcj 3.4.5, Groovy 1.7, Sun Java 6
Используется рекурсивное определение чисел Фибоначчи.
public class Fibonacci {
static int fibonacci(int n)
{
return (n<=2 ? 1 : fibonacci(n-1) + fibonacci(n-2));
}
public static void main(String[] args)
{
for (int n=1; n<=16; n++)
System.out.print(fibonacci(n)+", ");
System.out.println("...");
}
}
Пример для версий Microsoft Visual Basic 6
Используется рекурсивное определение чисел Фибоначчи.
Option Explicit
Declare Function AllocConsole Lib "kernel32" () As Long
Declare Function FreeConsole Lib "kernel32" () As Long
Declare Function CloseHandle Lib "kernel32" (ByVal hObject As Long) As Long
Declare Function GetStdHandle Lib "kernel32" (ByVal nStdHandle As Long) As Long
Declare Function WriteConsole Lib "kernel32" Alias "WriteConsoleA" _
(ByVal hConsoleOutput As Long, lpBuffer As Any, ByVal _
nNumberOfCharsToWrite As Long, lpNumberOfCharsWritten As Long, _
lpReserved As Any) As Long
Declare Function Sleep Lib "kernel32" (ByVal dwMilliseconds As Long) As Long
Public Function Fibonacci(ByVal n As Integer) As Integer
If (n <= 2) Then
Fibonacci = 1
Else
Fibonacci = Fibonacci(n - 1) + Fibonacci(n - 2)
End If
End Function
Private Sub Main()
'create a console instance
AllocConsole
'get handle of console output
Dim hOut As Long
hOut = GetStdHandle(-11&)
'output string to console output
Dim s As String
Dim i As Integer
For i = 1 To 16 Step 1
s = Fibonacci(i) & ", "
WriteConsole hOut, ByVal s, Len(s), vbNull, vbNull
Next i
s = "..." & vbCrLf
WriteConsole hOut, ByVal s, Len(s), vbNull, vbNull
'make a pause to look at the output
Sleep 2000
'close the handle and destroy the console
CloseHandle hOut
FreeConsole
End Sub
Пример для версий QBasic 1.1, QuickBasic 4.50
Используется рекурсивное определение чисел Фибоначчи. Каждый вызов команды PRINT выводит аргументы в отдельную строку и добавляет пробел перед и после выводимого числа. В результате вывод программы имеет следующий вид:
1 ,
1 ,
2 ,
3 ,
5 ,
8 ,
13 ,
21 ,
34 ,
55 ,
89 ,
144 ,
233 ,
377 ,
610 ,
987 ,
…
DECLARE FUNCTION fibonacci (n)
FOR i = 1 TO 16:
PRINT fibonacci(i); ", "
NEXT i
PRINT "..."
FUNCTION fibonacci (n)
IF (n <= 2) THEN
fibonacci = 1
ELSE
fibonacci = fibonacci(n - 1) + fibonacci(n - 2)
END IF
END FUNCTION
Пример для версий QBasic 1.1, QuickBasic 4.50
Уже вычисленные числа хранятся в массиве F и извлекаются оттуда для вычисления следующих. Для получения вывода программы в нужном формате числа в массиве конкатенируются в одну строку с нужными разделителями. Функция STR$ преобразует число в строку.
DIM F(16)
F(1) = 1
F(2) = 1
FOR i = 3 TO 16:
F(i) = F(i - 1) + F(i - 2)
NEXT i
DIM S AS STRING
S = ""
FOR i = 1 TO 16:
S = S + STR$(F(i)) + ", "
NEXT i
S = S + "..."
PRINT S
Пример для версий QBasic 1.1, QuickBasic 4.50
Числа Фибоначчи вычисляются через формулу Бине. За счет погрешностей вычисления с плавающей точкой полученные числа могут незначительно отличаться от действительных; для устранения этого эффекта используется функция INT, отбрасывающая дробную часть числа.
DECLARE FUNCTION FIBONACCI (n)
DIM S AS STRING
S = ""
FOR i = 1 TO 16:
S = S + STR$(INT(FIBONACCI(i) + .1)) + ","
NEXT i
S = S + "..."
PRINT S
FUNCTION FIBONACCI (n)
p1 = ((1 + SQR(5)) * .5) ^ n
p2 = ((1 - SQR(5)) * .5) ^ n
FIBONACCI = (p1 - p2) / SQR(5)
END FUNCTION
Пример для версий Oracle 10g SQL, Oracle 11g SQL
SQL не поддерживает циклы или рекурсии, кроме того, конкатенация полей из разных строк таблицы или запроса не является стандартной агрегатной функцией. Данный пример использует:
-
формулу Бине и математические функции
ROUND,POWERиSQRTдля вычисления n-ого числа Фибоначчи; -
псевдостолбец
levelдля создания псевдотаблицы t1, содержащей числа от 1 до 16; -
встроенную функцию
SYS_CONNECT_BY_PATHдля упорядоченной конкатенации полученных чисел.
SELECT REPLACE(MAX(SYS_CONNECT_BY_PATH(fib||', ', '/')),'/','')||'...' fiblist
FROM (
SELECT n, fib, ROW_NUMBER()
OVER (ORDER BY n) r
FROM (select n, round((power((1+sqrt(5))*0.5, n)-power((1-sqrt(5))*0.5, n))/sqrt(5)) fib
from (select level n
from dual
connect by level <= 16) t1) t2
)
START WITH r=1
CONNECT BY PRIOR r = r-1;
Пример для версий EsCo 0.511 (Brainfuck), Müller's Brainfuck 2.0, weave.rb
В примере используется итеративное определение чисел Фибоначчи: два последних числа хранятся в ячейках-переменных c4 и c5 (в начале c4=0, c5=1), число c5 посимвольно выводится на печать (это действие занимает большую часть кода), затем вычисляется следующее число (c6 = c5+c4), и числовая пследовательность сдвигается на одно число вперед (c4 = c5, c5 = c6). Низкоуровневое описание приведено в комментариях к коду, запись “cXvY” означает, что после выволнения команд в строке указатель данных находится в ячейке X, и значение в этой ячейке равно Y.
Классический интерпретатор Brainfuck использует переменные типа byte для хранения значений в ячейках памяти, и 14-16 числа Фибоначчи вызовут ошибку переполнения. Написание длинной арифметики на Brainfuck — задача достаточно трудоемкая, поэтому в примере предполагается, что в ячейках памяти могут храниться числа типа integer.
++++++++++++++++++++++++++++++++++++++++++++ c1v44 : ASCII code of comma
>++++++++++++++++++++++++++++++++ c2v32 : ASCII code of space
>++++++++++++++++ c3v11 : quantity of numbers to be calculated
> c4v0 : zeroth Fibonacci number (will not be printed)
>+ c5v1 : first Fibonacci number
<< c3 : loop counter
[ block : loop to print (i)th number and calculate next one
>> c5 : the number to be printed
block : divide c5 by 10 (preserve c5)
> c6v0 : service zero
>++++++++++ c7v10 : divisor
<< c5 : back to dividend
[->+>-[>+>>]>[+[-<+>]>+>>]<<<<<<] c5v0 : divmod algo; results in 0 n d_n%d n%d n/d
>[<+>-] c5 : move dividend back to c5 and clear c6
>[-] c7v0 : clear c7
>> block : c9 can have two digits; divide it by ten again
>++++++++++ c10v10: divisor
< c9 : back to dividend
[->-[>+>>]>[+[-<+>]>+>>]<<<<<] c9v0 : another divmod algo; results in 0 d_n%d n%d n/d
>[-] c10v0 : clear c10
>>[++++++++++++++++++++++++++++++++++++++++++++++++.[-]]c12v0 : print nonzero n/d (first digit) and clear c12
<[++++++++++++++++++++++++++++++++++++++++++++++++.[-]] c11v0 : print nonzero n%d (second digit) and clear c11
<<<++++++++++++++++++++++++++++++++++++++++++++++++.[-] c8v0 : print any n%d (last digit) and clear c8
<<<<<<<.>. c1c2 : print comma and space
block : actually calculate next Fibonacci in c6
>>[>>+<<-] c4v0 : move c4 to c6 (don't need to preserve it)
>[>+<<+>-] c5v0 : move c5 to c6 and c4 (need to preserve it)
>[<+>-] c6v0 : move c6 with sum to c5
<<<- c3 : decrement loop counter
]
<<++... c1 : output three dots
Пример для версий Microsoft SQL Server 2005, Microsoft SQL Server 2008 R2, Microsoft SQL Server 2012
Используется итеративное определение чисел Фибоначчи, реализованное через рекурсивный запрос. Каждая строка запроса содержит два соседних числа последовательности, и следующая строка вычисляется как (последнее число, сумма чисел) предыдущей строки. Таким образом все числа, кроме первого и последнего, встречаются дважды, поэтому в результат входят только первые числа каждой строки.
with fibonacci(a, b) as
(
select 1, 1
union all
select b, a+b from fibonacci where b < 1000
)
SELECT cast(a as varchar)+', ' AS [text()]
FROM fibonacci
FOR XML PATH ('')
Пример для версий iconc 9.4
Используется рекурсивное вычисление чисел Фибоначчи с мемоизацией промежуточных результатов
global fib_memo
procedure fib (n)
if n >= 0 then
return ((/fib_memo [n] := fib (n - 2) + fib (n - 1)) | fib_memo [n])
end
procedure main ()
local i
fib_memo := table ()
fib_memo [0] := 0; fib_memo [1] := 1
every i := 1 to 16 do {
writes (fib (i) || ", ")
}
write("...")
end
Пример для версий Interactive FP
Этот пример работает так же, как пример факториала, но без добавления функций для читабельности.
{ seq ( = @ [id, %1] -> %<1> ; concat @ [ seq @ - @ [id, %1] , [id] ] ) }
{ fibonacci ( < @ [id, %3] -> %1 ; + @ [ fibonacci @ - @ [id, %1], fibonacci @ - @ [id, %2] ] ) }
&fibonacci @ seq:16
Пример для версий clisp 2.47, Corman Common Lisp 3.0, gcl 2.6.6
Этот пример использует итеративное определение чисел Фибоначчи без запоминания, выраженное через рекурсивный вызов функции fib-iter.
(defun fibonacci (n)
(defun fib-iter (a b count)
(if (zerop count)
b
(fib-iter (+ a b) a (- count 1))
)
)
(fib-iter 1 0 n)
)
(loop for i from 1 to 16
do (format t "~D, " (fibonacci i))
finally (format t "...~%")
)
Пример для версий Visual Prolog 7.2
В этом примере определяются два новых предиката — бинарный fibonacci(N,F) для вычисления N-ого числа Фибоначчи и loop(N) для его вывода на печать. Единожды вычисленные числа не сохраняются для позднейшего использования, поэтому эта реализация неэффективна.
Следует отметить отличие реализаций предикатов от примера для факториала: формулы, описывающие начальные условия, задаются для произвольного значения переменной, но вычисляются до конца только в том случае, если первое правило (N<3 или N=1, соответственно) оценивается как истинное. Кроме того, каждый предикат записан как одна формула, использующая конъюнкцию и дизъюнкцию, а не как набор отдельных формул, использующих только конъюнкцию.
% main.cl
class main
open core
predicates
classInfo : core::classInfo.
fibonacci : (integer N, integer F) procedure (i,o).
loop : (integer N) procedure (i).
predicates
run : core::runnable.
end class main
% main.pro
implement main
open core
constants
className = "main".
classVersion = "".
clauses
classInfo(className, classVersion).
fibonacci(N,F) :-
N < 3, !, F = 1;
fibonacci(N-1,F1), fibonacci(N-2,F2), F = F1 + F2.
loop(N) :-
( N = 1, !, fibonacci(1,F);
loop(N-1), fibonacci(N,F) ),
stdio::write(F, ", ").
clauses
run():-
console::init(),
loop(16),
stdio::write("..."),
programControl::sleep(1000),
succeed().
end implement main
goal
mainExe::run(main::run).
Пример для версий Oracle 10g SQL, Oracle 11g SQL
Этот пример демонстрирует использование оператора model, доступного начиная с версии Oracle 10g и позволяющего обработку строк запроса как элементов массива. Каждая строка содержит два поля — само число Фибоначчи и конкатенация всех чисел, меньше или равных ему. Итеративная конкатенация чисел в том же запросе, в котором они генерируются, выполняется проще и быстрее, чем агрегация как отдельное действие.
select max(s) || ', ...'
from
(select s
from dual
model
return all rows
dimension by ( 0 d )
measures ( cast(' ' as varchar2(200)) s, 0 f)
rules iterate (16)
( f[iteration_number] = decode(iteration_number, 0, 1, 1, 1, f[iteration_number-1] + f[iteration_number-2]),
s[iteration_number] = decode(iteration_number, 0, to_char(f[iteration_number]), s[iteration_number-1] || ', ' || to_char(f[iteration_number]))
)
);
Пример для версий MySQL 5
Замените TABLE на любую таблицу, к которой есть доступ, например, mysql.help_topic.
select concat(group_concat(f separator ', '), ', ...')
from (select @f := @i + @j as f, @i := @j, @j := @f
from TABLE, (select @i := 1, @j := 0) sel1
limit 16) t
Пример для версий ARIBAS 1.53
Этот пример использует рекурсивное определение чисел Фибоначчи. В ARIBAS по умолчанию используется тип данных integer. group(0) при выводе служит для отмены использования знака подчеркивания для разделения групп цифр.
function fib(n);
begin
if (n < 3) then
return(1);
end;
return(fib(n-1)+fib(n-2));
end;
function fib1_16();
var n;
begin
for n := 1 to 16 do
write(fib(n): group(0), ", ");
end;
writeln("...");
end;
fib1_16().
Пример для версий VB.NET 9 (2008), vbnc 2.4.2
Используется рекурсивное определение чисел Фибоначчи.
Module Module1
Function Fibonacci(ByVal n As Integer) As Long
If n < 3 Then
Return 1
Else
Return Fibonacci(n - 1) + Fibonacci(n - 2)
End If
End Function
Sub Main()
For i As Integer = 1 To 16
Console.Write(Fibonacci(i) & ", ")
Next
Console.WriteLine("...")
End Sub
End Module
Пример для версий PHP 5.2.4, PHP 5.3.2
Используется рекурсивное определение чисел Фибоначчи.
<?php
function fibonacci($n)
{
if ($n < 3) {
return 1;
}
else {
return fibonacci($n-1) + fibonacci($n-2);
}
}
for ($n = 1; $n <= 16; $n++) {
echo(fibonacci($n) . ", ");
}
echo("...\n")
?>
Пример для версий Oracle 10g SQL, Oracle 11g SQL
Этот пример использует итеративное определение чисел Фибоначчи. Уже вычисленные числа хранятся в структуре данных varray — аналоге массива.
declare
type vector is varray(16) of number;
fib vector := vector();
i number;
s varchar2(100);
begin
fib.extend(16);
fib(1) := 1;
fib(2) := 1;
s := fib(1) || ', ' || fib(2) || ', ';
for i in 3..16 loop
fib(i) := fib(i-1) + fib(i-2);
s := s || fib(i) || ', ';
end loop;
dbms_output.put_line(s || '...');
end;
Пример для версий g95 0.93, gfortran 4.5.0, Intel Visual Fortran 11.1
Используется итеративное определение чисел Фибоначчи. Самое сложное в этом примере — вывод вычисленных значений в нужном формате, в одну строку и без лишних пробелов. Спецификация формата (I3, A, $) означает, что вначале выводится целое число в десятичном формате, шириной ровно три символа, затем выводится строка, и наконец, $ подавляет перевод строки, используемый командой print по умолчанию, так что все выводится в одну строку. Отметим, что в диалекте F спецификатор формата $ не является стандартным; программа работает, но при компиляции выводит предупреждение об этом.
program Fibonacci
integer :: f1,f2,f3,i
i = 1
f1 = 0
f2 = 1
do
f3 = f2 + f1
f1 = f2
f2 = f3
i = i + 1
if (f1 < 10) then
print "(I1, A, $)", f1, ", "
elseif (f1 < 100) then
print "(I2, A, $)", f1, ", "
else
print "(I3, A, $)", f1, ", "
end if
if (i == 17) then
exit
end if
end do
print *, "..."
end program Fibonacci
Пример для версий Poplog 15.5 (Prolog)
Простая рекурсивная реализация слишком неэффективна с точки зрения памяти, чтобы успешно выполняться в Poplog, поэтому этот пример демонстрирует более сложную технику — рекурсию с запоминанием. Дополнительный предикат memo(Goal) определяется так, что в первый раз, когда оценивается Goal, результат оценки добавляется в базу фактов, и при следующем запросе не переоценивается, а используется как известный факт.
После этого предикат fib(N,F) определяется рекурсивно, но каждый вызов fib “обернут” в предикат memo, поэтому для каждого значения N fib(N,F) оценивается только один раз. При таком подходе печать вычисленных чисел может производиться сразу после их вычисления, без дополнительного цикла.
% fibonacci.pl
:- dynamic(stored/1).
memo(Goal) :-
stored(Goal) -> true;
Goal, assertz(stored(Goal)).
fib(1,1) :- !, write('1, ').
fib(2,1) :- !, write('1, ').
fib(N,F) :-
N1 is N-1, memo(fib(N1,F1)),
N2 is N-2, memo(fib(N2,F2)),
F is F1 + F2,
write(F), write(', ').
% interactive
[-fibonacci].
fib(16,X), write('...'), nl.
Пример для версий Poplog 15.5 (POP-11)
Используется рекурсивное определение чисел Фибоначчи. Пример работает так же, как факториал, но loop возвращает строку, содержащую конкатенацию всех чисел Фибоначчи до n-ого включительно.
define fibonacci(n);
if n < 3
then 1
else fibonacci(n - 1) + fibonacci(n - 2)
endif
enddefine;
define loop(n);
if n>1
then loop(n-1) >< ', ' >< fibonacci(n)
else fibonacci(n)
endif;
enddefine;
loop(16) >< ', ...' =>
Пример для версий Lua 5.0
Используется рекурсивное определение чисел Фибоначчи.
function fibonacci(n)
if n<3 then
return 1
else
return fibonacci(n-1) + fibonacci(n-2)
end
end
for n = 1, 16 do
io.write(fibonacci(n), ", ")
end
io.write("...\n")
Пример для версий Lua 5.0
Вычисленные числа хранятся в ассоциативном массиве fib и извлекаются из него для вычисления следующих. По умолчанию ассоциативные массивы в Lua используют целочисленные ключи, начинающиеся с 1, поэтому команда fib = {1, 1} создает массив с индексами элементов 1 и 2.
fib = {1, 1}
for n = 3, 16 do
fib[n] = fib[n-1] + fib[n-2]
end
for n = 1, 16 do
io.write(fib[n], ", ")
end
io.write("...\n")
Пример для версий SpiderMonkey (Firefox 3.5)
Используется рекурсивное определение чисел Фибоначчи. Пример предназначен для запуска из веб-браузера.
function fibonacci(n)
{ if (n<3)
return 1;
else
return fibonacci(n-1) + fibonacci(n-2);
}
var i;
document.clear();
for (i = 1; i <= 16; i++)
document.write(fibonacci(i) + ", ");
document.write("...<br />");
Пример для версий GHC 6.10.4
Этот пример использует одну из основных особенностей языка Haskell — возможность ленивых вычислений и использования бесконечных списков. Бесконечный список чисел Фибоначчи fibs определяется при помощи фунции zipWith, которая применяет первый аргумент (функцию двух переменных, в данном случае +) к парам соответствующих элементов второго и третьего аргументов (списков). tail fibs возвращает хвост списка fibs (т.е. все элементы, кроме первого). Таким образом первый элемент списка, возвращаемого zipWith, является суммой первого и второго элементов списка fibs и становится третьим его элементом.
module Main where
import Text.Printf
fibs :: [Int]
fibs = 0 : 1 : zipWith (+) fibs (tail fibs)
line n = printf "%d, " $ fibs !! n
main = do
sequence_ $ map line [1..16]
putStrLn "..."
Пример для версий GHC 6.10.4
Этот пример использует рекурсивное определение чисел Фибоначчи через пары соседних чисел в последовательности. На печать выводятся только первые элементы пар.
module Main where
import Text.Printf
fibNextPair :: (Int, Int) -> (Int, Int)
fibNextPair (x, y) = (y, x+y)
fibPair :: Int -> (Int, Int)
fibPair n
| n == 1 = (1, 1)
| otherwise = fibNextPair (fibPair (n-1))
line n = printf "%d, " $ (fst.fibPair) n
main = do
sequence_ $ map line [1..16]
putStrLn "..."
Пример для версий Furry Paws
one = eq.[id, ~1]
dec = sub.[id, ~1]
seq = one -> [~1] ; cat.[seq.dec, [id]]
fibonacci = lt.[id, ~3] -> ~1 ; add.[fibonacci.sub.[id, ~1], fibonacci.sub.[id, ~2]]
main = show.(return @fibonacci.(seq.~16))
Пример для версий gnat 3.4.5
В этом примере используется рекурсивное определение чисел Фибоначчи.
with Ada.Text_IO, Ada.Integer_Text_IO;
procedure Fibonacci is
begin
declare
function Fib (N: Integer) return Integer is
begin
if N<3 then
return 1;
else
return Fib(N-1) + Fib(N-2);
end if;
end Fib;
i: Integer := 1;
begin
loop
Ada.Integer_Text_IO.Put (Item => Fib(i), Width => 1);
Ada.Text_IO.Put (", ");
i := i + 1;
exit when i=17;
end loop;
Ada.Text_IO.Put ("...");
end;
end Fibonacci;
Пример для версий UCBLogo 6.0
Используется рекурсивное определение чисел Фибоначчи. В примере определяются две функции — fibonacci для вычисления значения N-ого числа Фибоначчи и print_fibonacci, которая накапливает числа в строке и выводит их на печать.
to fibonacci :N
ifelse :N < 3 [output 1] [output sum fibonacci :N - 1 fibonacci :N - 2]
end
to print_fibonacci :i :N
make "str fibonacci :i
make "i sum :i 1
make "comma ",
repeat :N - :i + 1 [make "str (word :str :comma fibonacci :i)
make "i sum :i 1]
make "str word str ",...
print str
end
print_fibonacci 1 16
Пример для версий Scala 2.7.7-final
Используется рекурсивное определение чисел Фибоначчи.
object Fibonacci {
def fibonacci(n: Int): Int =
if (n < 3) 1
else fibonacci(n - 1) + fibonacci(n - 2)
def main(args: Array[String]) {
for {i <- List.range(1, 17)}
yield { print(fibonacci(i) + ", ") }
println("...")
}
}
Пример для версий Scala 2.7.7-final
Этот пример демонстрирует возможности использования ленивых вычислений и бесконечных списков в Scala. Бесконечный список чисел Фибоначчи fibs определяется при помощи фунций .zip и .tail по аналогии с примером на Haskell. Пример предназначен для интерактивной интерпретации.
lazy val fib: Stream[Int] = Stream.cons(1, Stream.cons(1, fib.zip(fib.tail).map(p => p._1 + p._2)))
fib.take(16).print
Пример для версий gawk 3.1.6, Jawk 1.02, mawk 1.3.3
Используется итеративное определение чисел Фибоначчи. fib — ассоциативный массив, pr — строка.
BEGIN {
fib[1] = 1
fib[2] = 1
for (i=3; i<17; i++)
fib[i] = fib[i-1]+fib[i-2]
pr = ""
for (i=1; i<17; i++)
pr = pr fib[i] ", "
print pr "..."
}
Пример для версий S-lang 2.2.2
В примере используется итеративное определение чисел Фибоначчи. Переменная f явно определена как массив 16 целых чисел. Элементы 0 и 1 массива устанавливаются в 1: для этого операцией [0:1] создается список индексов, к которым следует применить операцию. Встроенная функция string преобразует свой аргумент в его строковое представление.
f = Integer_Type [16];
f[[0:1]] = 1;
for (i=2; i<16; i++)
f[i] = f[i-1] + f[i-2];
s = "...";
for (i=15; i>=0; i--)
s = string(f[i]) + ", " + s;
message (s);
Пример для версий Hanoi Love
В примере используется итеративное определение чисел Фибоначчи.
Стек A большую часть времени пуст и используется для получения константы 1; иногда используется для временного хранения значений (по тому же принципу, что и в оригинальной задаче о Ханойских башнях). Стек B содержит символы, выводимые на печать (запятую и пробел) и два последних числа Фибоначчи из вычисленных программой. Стек C содержит значение 1 для каждого числа Фибоначчи, которое нужно напечатать (в данном случае шесть единиц для печати 6 чисел).
На каждой итерации одно число извлекается из стека C. Если оно положительно (т.е. нужно вычислить и напечатать еще одно число Фибоначчи), верхнее число f2 из стека B извлекается, преобразуется в ASCII-код соответствующей цифры и выводится на печать вместе с запятой и пробелом. После этого следующее число f1 извлекается из стека B и прибавляется к числу f2. Наконец, числа f2 и f1+f2 возвращаются в стек B. Низкоуровневое описание примера приводится в комментариях.
Интерпретатор Hanoi Love использует переменные типа byte для хранения значений в регистре и стеках, поэтому принципиально возможно вычислить только первые 13 чисел Фибоначчи. В действительности пример выводит только первые 6 чисел Фибоначчи, чтобы не усложнять программу печатью двух- и трехзначных чисел (которая выполняется по тому же принципу, что и в Brainfuck, но сложнее).
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; .' B (space) regr = ASCII for space
...;;;;;;;;;;;;.' B (space comma) reg = ASCII for comma
..., A (empty) reg = 1
..'''''' C (6 ones for 6 numbers to print) reg = 1
..`.'...;.' B (space comma 0 1) reg = 1
., C (pop number to reg) reg = 1
.'... D (remembered this place)
: if this number is positive print top number in B and move to next Fibonacci number
..., B (space comma f1) reg = f2
.' C (f2) reg = f2
..;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; "' A (empty) reg = f2 in ASCII (printed)
., B (space comma) reg = f1
.' C (f2 f1) reg = f2
..., "' B (space) reg = comma (printed)
.' C (f2 f1 comma) reg = comma
..., "' ' B (space) reg = space (printed)
.,...' B (space comma) reg = comma
., C (f2) reg = f1
..' A (f1) reg = f1
.., C (empty) reg = f2
...' B (space comma f2) reg = f2
...; A (empty) reg = f1+f2
.' B (space comma f2 f1+f2)
., C (pop number to reg)
., D (get previous command location)
!
...,,,...;; "' "' "' pop everything from B and convert comma to point (printed three times)
Пример для версий J602
В этом примере используется формула Бине.
Запись g =: -: >: %:5 эквивалентна g =: 0.5 * (1 + 5 ^ 0.5) и присваивает имя g значению золотого сечения. Для этого используются следующие функции: %: извлекает квадратный корень из числа, >: увеличивает число на единицу, -: делит число на два. Если в формуле нет скобок, то действия выполняются справа налево.
Запись fibb=: (%:5) %~ g&^ — (1-g)&^ эквивалентна fibb =: (0.2 ^ 0.5) * (g &^ — (1-g) &^); таким образом определяется формула для n-ого числа Фибоначчи при заданном n. Функция %~ выполняет операцию деления, но делимое и делитель имеют порядок, обратный традиционному.
i.16 генерирует числа от 0 до 15, включительно.
load 'printf'
g=: -: >: %:5
fibb=: (%:5) %~ g&^ - (1-g)&^
fstr=: '...' ,~ ,~^:4 '%d, '
fstr printf fibb 1+i.16
Пример для версий J602
В этом примере используется рекурсивное определение чисел Фибоначчи. Оператор @. — селектор, выбирающий 1, если аргумент функции меньше или равен 2, и рекурсивное определение в противном случае.
load 'printf'
fibr=: 1:`(-&2 + &fibr -&1) @.(2&<)"0
fstr=: '...' ,~ ,~^:4 '%d, '
fstr printf fibr 1+i.16
Пример для версий Mathics 0.4, Wolfram Mathematica 7.0.1.0, Wolfram Mathematica 8.0.4
Print обязательно завершает вывод переносом строки, поэтому для того, чтобы вывести все числа Фибоначчи в одной строке, их нужно накопить в переменной msg и вывести ее. <> — оператор конкатенации; он работает только с явными строками, поэтому результат вызова Fibonacci нужно явно перевести в строку функцией ToString.
msg = "";
Do[msg = msg <> ToString[Fibonacci[i]] <> ", " , {i, 16} ];
Print[msg, "..."];
Пример для версий Mercury 10.04
Вычисление и вывод на экран десятого числа последовательности Фибоначчи.
:- module fib.
:- interface.
:- import_module io.
:- pred main(io::di, io::uo) is det.
:- implementation.
:- import_module int.
:-func fib(int) = int.
fib(N) = (if N =< 2 then 1 else fib(N - 1) + fib(N - 2)).
main(!IO) :-
io.write_string("fib(10) = ", !IO),
io.write_int(fib(10), !IO),
io.nl(!IO).
% Could instead use io.format("fib(10) = %d\n", [i(fib(10))], !IO).
Пример для версий Whitespacers (Ruby)
Пример работает аналогично факториалу, но интенсивнее использует хранение данных в стеке и команду копирования верхнего элемента стека, чтобы избежать лишних обращений к памяти. Кроме того, в этом примере счетчик отрицательный и увеличивается на каждой итерации.
push_1 { }
push_-16 { }
store push_2 { }
push_44 { }
store push_3 { }
push_32 { }
store push_4 { }
push_0 { }
store push_5 { }
push_1 { }
store label
{ }
start_loop_push_5 { }
push_4 { }
retrieve push_4 { }
duplicate
push_5 { }
retrieve duplicate
print_as_number
push_2 { }
retrieve print_as_char
push_3 { }
retrieve print_as_char
store retrieve add store push_1 { }
duplicate
duplicate
duplicate
retrieve add store retrieve jump_if_negative
{ }
push_10 { }
push_46 { }
duplicate
duplicate
print_as_char
print_as_char
print_as_char
print_as_char
quit
end
Пример для версий erl 5.7.3
Используется итеративное определение чисел Фибоначчи, выраженное в форме хвостовой рекурсии.
-module(prog).
-export([main/0]).
fib(1,_,Res) ->
io:format("~B, ",[Res]);
fib(N,Prev,Res) when N > 1 ->
io:format("~B, ",[Res]),
fib(N-1, Res, Res+Prev).
main() ->
fib(16,0,1),
io:format("...~n").
Пример для версий erl 5.7.3
Используется формула Бине. Числа с плавающей точкой обязаны выводиться с как минимум одним знаком после запятой, поэтому результат работы выглядит так:
1.0, 1.0, 2.0, 3.0, 5.0, 8.0, 13.0, 21.0, 34.0, 55.0, 89.0, 144.0, 233.0, 377.0, 610.0, 987.0, ...
-module(prog).
-export([main/0]).
fib(0) -> ok;
fib(N) ->
fib(N-1),
SQ5 = math:sqrt(5),
T1 = math:pow(0.5*(1 + SQ5),N),
T2 = math:pow(0.5*(1 - SQ5),N),
io:format("~.1f, ", [(T1-T2)/SQ5]).
main() ->
fib(16),
io:format("...~n").
Пример для версий GDC 0.24
Используется рекурсивное определение чисел Фибоначчи.
module fibonacci;
import std.stdio;
ulong recursive(ulong x)
{
return x <= 2 ? 1 : recursive( x - 2 ) + recursive( x - 1 );
}
int main()
{
for (uint i = 1; i < 17; i++)
{
writef("%s, ", recursive(i));
}
writefln("%s", "...");
return 0;
}
Пример для версий GDC 0.24
Используется итеративное определение чисел Фибоначчи.
module fibonacci;
import std.stdio;
ulong iterative(ulong x)
{
ulong prev1 = 1L;
ulong prev2 = 1L;
ulong result = x <= 2 ? 1L : 0L;
for ( ulong i = 3; i <= x; ++i )
{
result = prev1 + prev2;
prev1 = prev2;
prev2 = result;
}
return result;
}
int main()
{
for (uint i = 1; i < 17; i++)
{
writef("%s, ", iterative(i));
}
writefln("%s", "...");
return 0;
}
Пример для версий Perl 5.12.1
Используется рекурсивное определение чисел Фибоначчи.
sub fibonacci {
my $n = shift;
$n < 3 ? 1 : fibonacci($n-1) + fibonacci($n-2)
}
foreach (1..16) {
print fibonacci($_), ", ";
}
print "..."
Пример для версий Ruby 1.8.5, Ruby 1.9.0, Ruby 1.9.2
Используется рекурсивное определение чисел Фибоначчи.
def fibonacci(n)
if n < 3
1
else
fibonacci(n - 1) + fibonacci(n - 2)
end
end
(1..16).each {|n| puts "#{fibonacci(n)}, "}
puts "..."
Пример для версий gmcs 2.0.1
Используется рекурсивное определение чисел Фибоначчи.
using System;
class Program
{
static long Fibonacci(int n)
{
if (n < 3)
return 1;
else
return Fibonacci(n - 1) + Fibonacci(n - 2);
}
static void Main(string[] args)
{
for (int i = 1; i < 17; i++)
Console.Write("{0}, ", Fibonacci(i));
Console.WriteLine("...");
}
}
Пример для версий gcc 3.4.5, gcc 3.4.5 (Objective-C), TCC 0.9.25
Используется рекурсивное определение чисел Фибоначчи.
#include <stdio.h>
int fibonacci(int n)
{
return ( n<=2 ? 1 : fibonacci(n-1) + fibonacci(n-2) );
}
int main(void)
{
int n;
for (n=1; n<=16; n++)
printf("%d, ", fibonacci(n));
printf("...\n");
return 0;
}
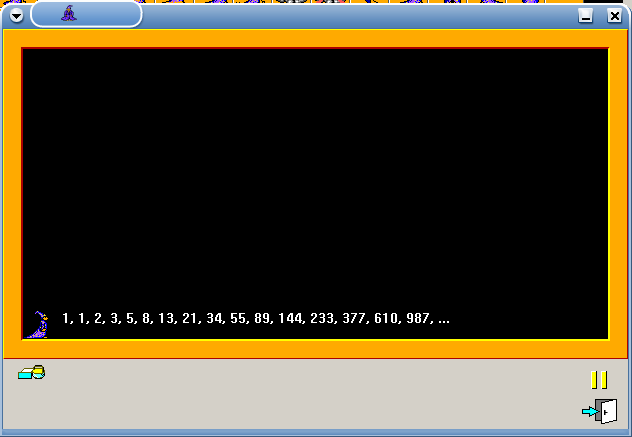
Пример для версий Scratch 1.4
В Scratch нет простого способа определить функцию, поэтому используется итеративное определение чисел Фибоначчи.
set f1 to 1
set f2 to 1
set str to f1
repeat 15
set f3 to (f1 + f2)
set f1 to f2
set f2 to f3
set str to join (str (join (,) f1))
say join (str (...))
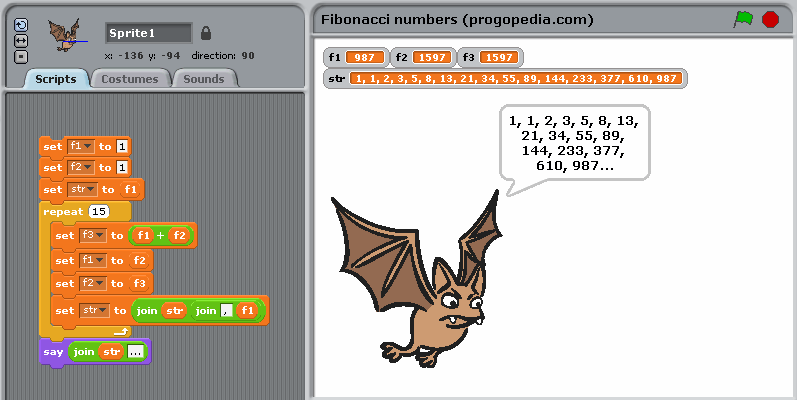
Числа Фибоначчи на Scratch
Пример для версий Sanscript 2.2
Числа Фибоначчи вычисляются так же, как факториал: цикл-Repeat вычисляет список чисел, начиная с двух первых, после чего список конкатенируется в выводимое сообщение. Внутри цикла текущее число добавляется к списку и заменяется на следующее, а следующее — на сумму текущего и следующего.
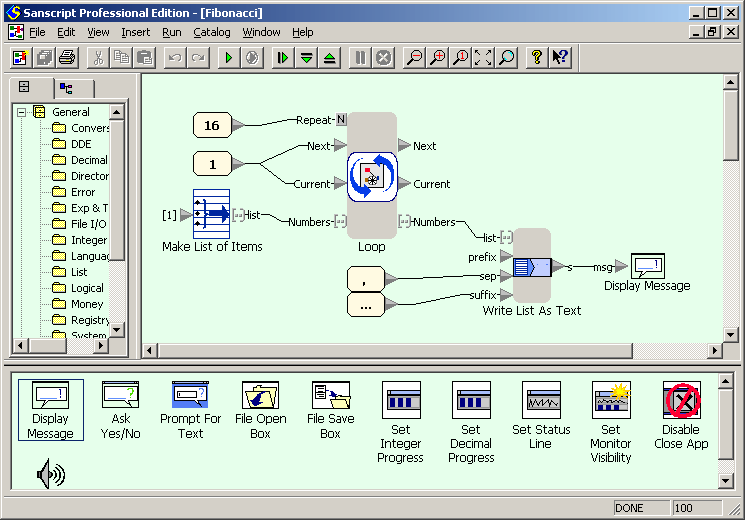
Числе Фибоначчи на Sanscript - главная диаграмма потоков
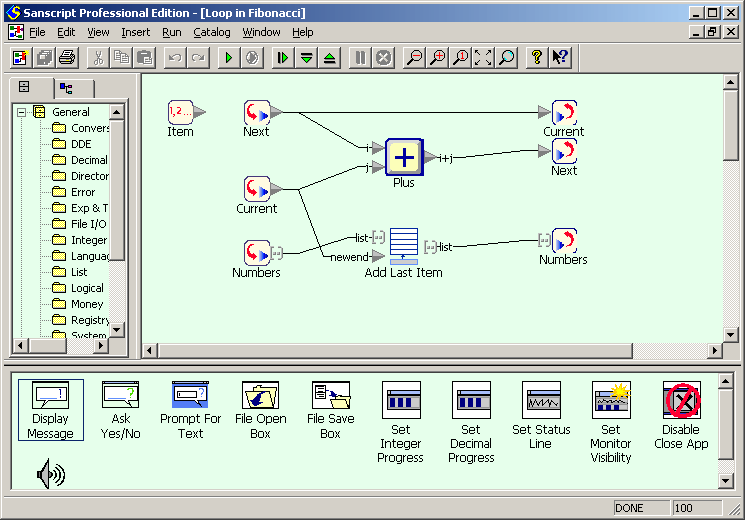
Числе Фибоначчи на Sanscript - блок Repeat
Пример для версий gc-2010-07-14
В этом примере показаны все три способа вычисления чисел Фибоначчи.
package main
import ("fmt"
"math")
//Fibonacci Recursive
func fibr(n int) int {
if n < 2 { return 1 }
return fibr(n-2) + fibr(n-1)
}
//Fibonacci Iterative
func fibi(n int) int {
var a, b int = 1, 1
for i := 0; i < n; i++ {
a, b = b, a+b
}
return a
}
//Fibonacci Binet
func fibb(n int) int {
g := (1 + math.Sqrt(5)) / 2
ret := (math.Pow(g, float64(n)) - math.Pow(1-g, float64(n))) / math.Sqrt(5)
return int(ret)
}
type fibfunc func(int) int
//Implements a general printing method for fibonacci functions
func printFib(fib fibfunc, a, b int) {
for i := a; i < b; i++ {
fmt.Printf("%d, ", fib(i))
}
fmt.Println("...")
}
func main() {
printFib(fibr, 0, 16)
printFib(fibi, 0, 16)
printFib(fibb, 1, 17)
}
Пример для версий GNU bc 1.06
Используется рекурсивное определение чисел Фибоначчи.
define fibonacci(n) {
if (n <= 2) return(1);
return(fibonacci(n-1)+fibonacci(n-2));
}
for (n = 1; n <= 16; n++) {
print fibonacci(n); ", "
}
print "..."
quit
Пример для версий GNU bc 1.06
Используется формула Бине. Следует отметить, что bc — калькулятор произвольной точности, поэтому выводить числа приходится с округлением до целого. Для этого устанавливается точность 0 знаков после десятичной точки, и x округляется вручную (встроенной функции округления в bc нет).
for (n = 1; n <= 16; n++) {
scale = 10
x = (((1 + sqrt(5)) * .5) ^ n - ((1 - sqrt(5)) * .5) ^ n) / sqrt(5)
scale = 0
print (x+0.5)/1; ", "
}
print "..."
Пример для версий B-Prolog 7.4-3, gprolog 1.3.0, swipl 5.6.x
Пример почти идентичен примеру для Poplog Prolog, за исключением синтаксиса подключения файла.
% fibonacci.pl
:- dynamic(stored/1).
memo(Goal) :-
stored(Goal) -> true;
Goal, assertz(stored(Goal)).
fib(1,1) :- !, write('1, ').
fib(2,1) :- !, write('1, ').
fib(N,F) :-
N1 is N-1, memo(fib(N1,F1)),
N2 is N-2, memo(fib(N2,F2)),
F is F1 + F2,
write(F), write(', ').
% interactive
[fibonacci].
fib(16,X), write('...'), nl.
Пример для версий gnuplot 4.2.2
Используется итеративное определение чисел Фибоначчи. В gnuplot этой версии нет циклов, поэтому цикл имитируется вызовом другого файла. Если печатать числа отдельными командами, они будут выводиться на отдельных строках, поэтому для накопления вычисленных чисел используется строка, которая выводит на печать все сразу после конца цикла.
### run.gp
#!/usr/bin/env gnuplot
i = 1
a = 1
b = 1
res = ''
load "fibonacci.gp"
print res, '...'
### fibonacci.gp
res = res . a . ', '
c = a
a = b
b = b+c
i = i+1
if (i <= 16) reread
Пример для версий boo 0.8.2
Используется итеративное определение чисел Фибоначчи.
a = array(int, 16)
a[0] = a[1] = 1
for i in range(2,16):
a[i] = a[i-1] + a[i-2]
s=""
for i in range(16):
s = s + a[i] + ", "
print(s + "...")
Пример для версий boo 0.8.2
В этом примере показано использование генератора fib — конструкции, которая инициализирует внутренние переменные a и b и при каждом следующем обращении изменяет их значения и выдает наружу. Функция zip “склеивает” элементы двух перечислений (в данном случае range(16) и генератора) в пары, создавая новое перечисление.
def fib():
a, b = 0, 1
while true:
yield b
a, b = b, a + b
s=""
for i, n in zip(range(16), fib()):
s = s+n+", "
print(s+"...")
Пример для версий gforth 0.7.0
Используется итеративное определение чисел Фибоначчи.
: fib-iter
0 1 rot 0 ?do over + swap loop drop ;
: lp
1 do
i dup fib-iter . ." , "
loop drop ;
17 lp
." ..."
Пример для версий gforth 0.7.0
Используется рекурсивное определение чисел Фибоначчи.
: fib-rec
dup 2 u< if exit then
1- dup recurse swap 1- recurse + ;
: lp
1 do
i dup fib-rec . ." , "
loop drop ;
17 lp
." ..."
Пример для версий C-INTERCAL 28.0, J-INTERCAL 0.11, J-INTERCAL 0.12
Используется итеративное определение чисел Фибоначчи. В переменных .11 и .12 хранятся предыдущее и текущее числа, в .9 — количество остающихся итераций.
Тело цикла довольно простое — напечатать число .11, скопировать .10 и .11 в .1 и .2, сложить их ((1009) NEXT вызывает сложение из стандартной библиотеки и записывает сумму в .3) и обновить значения. Самая сложная часть программы — код, обеспечивающий циклическое поведение. Вот что он делает:
(3) NEXT и (4) NEXT обеспечивают переход на метку (4). Здесь счетчик цикла .9 уменьшается на 1 (вызов (1010)). После этого .1 вычисляется побитовыми операциями и становится 1, если .9 содержит ненулевое значение, и 0 в противном случае, и затем увеличивается на 1. Наконец, RESUME .1 возвращает выполнение программы к одному из более ранних NEXT. Если .1 равно 2, программа возвращается на два NEXT назад и продолжает выполняться с DO (1) NEXT, возвращаясь к началу тела цикла. Если же .1 равно 1, программа возвращается на один NEXT назад, продолжает выполняться с PLEASE GIVE UP и останавливается.
Вывод программы выглядит следующим образом:
I
I
II
III
V
VIII
XIII
XXI
XXXIV
LV
LXXXIX
CXLIV
CCXXXIII
CCCLXXVII
DCX
CMLXXXVII
DO .9 <- #16
DO .10 <- #0
DO .11 <- #1
(1) PLEASE READ OUT .11
DO .1 <- .10
DO .2 <- .11
PLEASE (1009) NEXT
DO .10 <- .11
DO .11 <- .3
DO (3) NEXT
DO (1) NEXT
(3) DO (4) NEXT
PLEASE GIVE UP
(4) DO .1 <- .9
DO .2 <- #1
PLEASE (1010) NEXT
DO .9 <- .3
DO .1 <- '.9~.9'~#1
PLEASE (1020) NEXT
DO RESUME .1
Пример для версий BlackBox Component Builder 1.5
Используется рекурсивное определение чисел Фибоначчи.
MODULE Fibonacci;
IMPORT StdLog;
PROCEDURE fibonacci(n: INTEGER): INTEGER;
BEGIN
IF n < 3 THEN
RETURN 1;
ELSE
RETURN fibonacci(n-1)+fibonacci(n-2)
END;
END fibonacci;
PROCEDURE Do*;
VAR
n: INTEGER;
BEGIN
FOR n := 1 TO 16 DO
StdLog.Int(fibonacci(n));
StdLog.String(', ');
END;
StdLog.String('...');
StdLog.Ln;
END Do;
END Fibonacci.
Fibonacci.Do
Пример для версий Mozart 1.4.0
Используется рекурсивное определение чисел Фибоначчи. Отметим, что в языке Oz значения переменным можно присваивать только один раз, поэтому для накопления вывода приходится использовать тип Cell — контейнер на один элемент.
functor
import
Application System
define
fun{Fib N}
fun{Loop N A B}
if N == 0 then
B
else
{Loop N-1 A+B A}
end
end
in
{Loop N 1 0}
end
local
S
in
S = {NewCell ""}
for I in 1..16 do
S := {Append {Append @S {Int.toString {Fib I}}} ", "}
end
{System.showInfo {Append @S "..."}}
{Application.exit 0}
end
end
Пример для версий Mozart 1.4.0
Используется итеративное определение чисел Фибоначчи.
functor
import
Application System
define
local
A B C S
in
A = {NewCell 0}
B = {NewCell 1}
C = {NewCell 0}
S = {NewCell ""}
for I in 1..16 do
C := @A + @B
A := @B
B := @C
S := {Append {Append @S {Int.toString @A}} ", "}
end
{System.showInfo {Append @S "..."}}
{Application.exit 0}
end
end
Пример для версий GHC 6.8.1
Этот пример также использует ленивые вычисления, но иначе формирует вывод нужного формата.
main = putStrLn $ withDots $ join $ take 16 fibs
where fibs = 1 : 1 : zipWith (+) fibs (tail fibs)
join = foldl (\a b -> a ++ show b ++ ", " ) ""
withDots = (++ "...")
Пример для версий gst 3.1
Используется итеративное определение чисел Фибоначчи.
a1 := 0.
a2 := 1.
0 to: 15 do: [ :i |
a2 display.
t := a1 + a2.
a1 := a2.
a2 := t.
', ' display
]
'...' displayNl.
Пример для версий Müller's Brainfuck 2.0
Этот пример является переводом на Unary этого примера. Сам код слишком обширен, чтобы приводить его полностью, поэтому указана только его длина.
A string of
146778148267671308907956810331954494567788969820594569869966345643952713144
716974835554679004232198811425384864927587749892052914319949694507679080918
662111668706252645905597146857061868763596677983948203224834326028677131466
814323099384842068831692029352209655371798175735992788874417787727414767365
600708388513171998134124513036377960362194431944262896105838957344640161915
106378867996851411865254464299481964724009334722033995112813417289458551426
925973669722270280516592327343992579166227546099835941334220 zeros (approximately 1.5*10^509)
Пример для версий ActiveTcl 8.5, Tcl 8.5.7
Используется итеративное определение чисел Фибоначчи. lassign присваивает последовательные элементы списка, переданного в качестве первого аргумента (в данном случае — созданного командой [list ...]), переменным, заданным следующими аргументами (fib1 и fib2). Эта команда была перенесена в основной язык в версии Tcl 8.5, до того она входила в пакет TclX.
set fib1 0
set fib2 1
set s ""
for {set i 0} {$i < 16} {incr i} {
lassign [list $fib2 [incr fib2 $fib1]] fib1 fib2
append s "$fib1, "
}
puts "$s..."
Пример для версий ActiveTcl 8.5, Tcl 8.5.7
Для вычисления чисел Фибоначчи используется рекурсия. Функция fib определяется в пространстве имен tcl::mathfunc, для того, чтобы ее можно было использовать как функцию в выражениях expr.
proc tcl::mathfunc::fib {n} {
if {$n<=1} {
return 1
} else {
return [expr fib([expr {$n - 1}]) + fib([expr {$n - 2}])]
}
}
set s ""
for {set i 0} {$i < 16} {incr i} {
append s [expr fib($i)] ", "
}
puts "$s..."
Пример для версий Bash 3.0, Bash 4.0.35, Bash 4.1.5
Используется итеративное определение чисел Фибоначчи.
a=0
b=1
for (( n=1; $n<=16; n=$n+1 ));
do
a=$(($a + $b))
echo -n "$a, "
b=$(($a - $b))
done
echo "..."
Пример для версий Miller's Hack VM (JavaScript), Miller's Hack VM (Python)
Этот пример использует итерацию и работает так же, как в других эзотерических языках: ячейка памяти 0 хранит оставшееся количество чисел для вычисления, ячейки 1 и 2 хранят ASCII-коды запятой и пробела, ячейки 3 и 4 — два последних рассчитанных числа Фибоначчи. В цикле извлекаются значения ячеек 3 и 4, суммируются, новое значение выводится на печать, а ячейки памяти обновляются. После этого количество оставшихся чисел уменьшается на 1, и если оно становится 0, счетчик программы (эквивалент указателя инструкций в Brainfuck) перемещается на 6 символов вперед и выходит из цикла, в противном случае он возвращается обратно к началу цикла. Наконец, выводятся три точки.
27*0> 92+4*1> 84*2> 10^p3> 1<P 2<P 10^p4> 1<P 2<P 3< 4< + 0^p 4< 3> 4> 0< 1- 0> 0< 6? 67*c 58*6+0^0^PPP
Пример для версий Roco 20071014
Используется итеративное определение чисел Фибоначчи. Все числа хранятся в ячейках [2]..[17]. В ячейке [0] хранится номер следующего числа, ячейка [1] используется как временная переменная. Циклы реализованы как сопрограммы, поскольку по определению каждая сопрограмма выполняется циклически, до вызова другой сопрограммы или прерывания текущей.
co calc{
/* break the loop when the counter is 2+16, since numbers start with cell 2 */
eq [1] [0] 18
if [1] ac
/* calculate next number and store it to [[0]]*/
sub [1] [0] 1
set [[0]] [[1]]
sub [1] [0] 2
add [[0]] [[0]] [[1]]
/* output */
iout [[0]]
cout 44
cout 32
/* increment counter */
add [0] [0] 1
}
/* initialize with first Fibonacci numbers */
set [0] 4
set [2] 1
set [3] 1
iout [2]
cout 44
cout 32
iout [3]
cout 44
cout 32
ca calc
cout 46
cout 46
cout 46
ac
Пример для версий fsharp 2.0.0
Используется рекурсивное определение чисел Фибоначчи “в лоб”.
let rec fibonacci n =
match n with
| 1 | 2 -> 1
| _ -> fibonacci (n-1) + fibonacci (n-2)
let rec printFib n =
match n with
| 1 -> printf "%d, " (fibonacci (n))
| _ -> printFib (n-1)
printf "%d, " (fibonacci (n))
printFib(16)
printfn "..."
Пример для версий ncc 0.9.3
Используется рекурсивное определение чисел Фибоначчи, записанное в функциональном стиле. Следует отметить объявление счетчика цикла i — ключевое слово mutable, в отличие от обычного def, означает, что переменная будет изменяться.
def fib(i)
{
| x when x<2 => 1
| _ => fib(i - 2) + fib(i - 1)
}
mutable i=0;
while (i<16)
{ System.Console.Write("{0}, ", fib(i));
i++;
}
System.Console.WriteLine("...");
Пример для версий Web2c 2009
Данный пример использует итеративный процесс для расчета чисел Фибоначчи.
В макросе \fibonacci используются двойные фигурные скобки, т.к. в макросе присутствует цикл, который вызывается внутри другого цикла.
\newcount\n \newcount\np \newcount\npp \newcount\m \newcount\f
\def\fibonacci#1{{\ifnum #1<3 1\else
\np=1\npp=1\m=3
\loop\ifnum\m<#1\f=\npp\npp=\np\advance\np by\f\advance\m by 1\repeat
\f=0\advance\f by\np\advance\f by\npp
\number\f\fi}}
\def\printfibonacci#1{\m=#1\advance\m by 1
\n=1
\loop\ifnum\n<\m\fibonacci{\n}, \advance\n by 1\repeat...}
\printfibonacci{16}
\bye
Пример для версий EsCo 0.511 (Brainfuck)
Пример на COW. Аналогичен этому примеру, но вывод чисел на печать существенно упрощается за счет команды OOM; фактически, даже с более длинными командами пример лаконичнее исходного.
MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO
MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO
c1v44 : ASCII code of comma
moO MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO
MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO
c2v32 : ASCII code of space
moO MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO MoO
c3v11 : quantity of numbers to be calculated
moO c4v0 : zeroth Fibonacci number (will not be printed)
moO MoO c5v1 : first Fibonacci number
mOo mOo c3 : loop counter
MOO block : loop to print (i)th number and calculate next one
moO moO OOM c5 : the number to be printed
mOo mOo mOo mOo Moo moO Moo c1c2 : print comma and space
block : actually calculate next Fibonacci in c6
moO moO MOO moO moO MoO mOo mOo MOo moo c4v0 : move c4 to c6 (don't need to preserve it)
moO MOO moO MoO mOo mOo MoO moO MOo moo c5v0 : move c5 to c6 and c4 (need to preserve it)
moO MOO mOo MoO moO MOo moo c6v0 : move c6 with sum to c5
mOo mOo mOo MOo c3 : decrement loop counter
moo
mOo mOo MoO MoO Moo Moo Moo c1 : output three dots
Пример для версий Baltie 3
Используется итеративный способ вычисления чисел Фибоначчи. Иконки A..D — глобальные переменные (голубые — целочисленные, желтые — строковые). Стрелка влево — оператор присваивания. Цикл for получает в качестве аргументов переменную-счетчик цикла, начало и конец интервала. Иконка с двойной кавычкой — преобразование числовой переменной в строку.
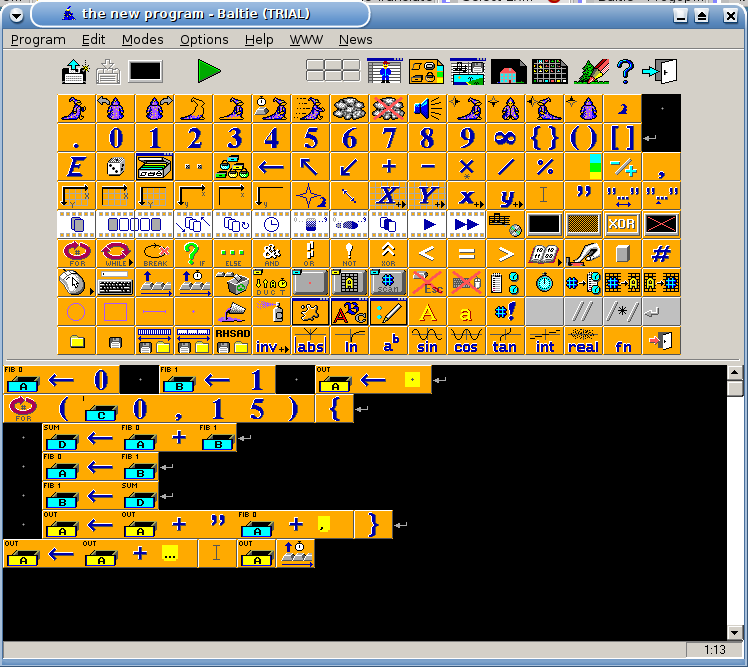
Числа Фибоначчи на Baltie 3
Числа Фибоначчи на Baltie 3 (результат)
Пример для версий Io-2008-01-07
В этом примере используется итерачивное вычисление чисел Фибоначчи. В цикле for пропущен четвертый аргумент, задающий шаг цикла — по умолчанию он равен 1.
N0 := 0;
N1 := 1;
for(i,1,16,
N2 := N1+N0;
N0 := N1;
N1 := N2;
N0 print;
", " print;
);
"..." println;
Пример для версий Io-2008-01-07
В этом примере для вычисления чисел Фибоначчи используется формула Бине. Математические функции также вызываются посредством передачи сообщения объекту-числу.
g := (5 sqrt + 1) / 2;
for(i,1,16,
N := ((g pow(i)) - ((1-g) pow(i))) / (5 sqrt);
N round print;
", " print;
);
"..." println;
Пример для версий Objective Caml 3.10.2
Используется рекурсивный метод вычисления чисел Фибоначчи.
let rec fibonacci n =
if n < 3 then
1
else
fibonacci (n-1) + fibonacci (n-2)
let () =
for n = 1 to 16 do
Printf.printf "%d, " (fibonacci n)
done;
print_endline "..."
Пример для версий MLton 20070826, Moscow ML 2.01, SML/NJ 110.69
Используется итеративное определение чисел Фибоначчи.
val n = ref 0;
val fib0 = ref 1;
val fib1 = ref 1;
val sum = ref 0;
val res = ref "";
while !n <= 15 do (
res := !res ^ (Int.toString(!fib0) ^ ", ");
sum := !fib0 + !fib1;
fib0 := !fib1;
fib1 := !sum;
n := !n + 1
);
print (!res ^ "...\n");;
Пример для версий Online Cat 1.3
В этом примере используется рекурсивное определение чисел Фибоначчи. Прежде всего определяется функция fib, работающая следующим образом.
При вызове функции верхний элемент стека N — номер числа, которое нужно вычислить (это единственный способ передать аргумент в функцию в Cat). Последовательность команд dup 1 <= копирует верхний элемент, сравнивает его с 1 и добавляет в стек true, если он меньше или равен 1, и false в противном случае. Затем следует условное выражение: в стек добавляются две последовательности команд (выделенные в блоки [...]), и если третий сверху элемент стека — true, выполняется первая из них, иначе — вторая. В данном случае последовательность для true пуста (Fib(0)=0, Fib(1)=1, и вычисления не нужны), последовательность для false следующая. Скопировать верхний элемент стека (это снова N), уменьшить его на 1, вызвать функцию fib для N-1, которая заменит N-1 на Fib(N-1). Затем поменять местами два верхних элемента стека (Fib(N-1) N), уменьшить верхний элемент на 2 и вызвать функцию fib, которая заменит его на Fib(N-2). Наконец, два верхних элемента стека суммируются, чтобы получить искомое Fib(N).
Вторая часть программы — цикл while по индексам от 1 до 16, который вычисляет числа и выводит их на печать. Тело цикла [dup fib write ", " write inc] копирует верхний элемент стека, вычисляет соответствующее число Фибоначчи, печатает его и запятую после него и увеличивает счетчик цикла. [dup 16 lteq] — условие повторения цикла: счетчик меньше или равен 16.
define fib {
dup 1 <=
[]
[dup 1 - fib swap 2 - fib +]
if
}
1
[dup fib write ", " write inc]
[dup 16 lteq]
while
"..." writeln
Пример для версий 64-bit BCPL Cintcode System (1 Nov 2006)
Используется рекурсивный метод вычисления чисел Фибоначчи.
GET "libhdr"
LET start() = VALOF
{ FOR i = 0 TO 15 DO writef("%n, ", fibonacci(i))
writef("...*n")
RESULTIS 0
}
AND fibonacci(n) = n<2 -> 1, fibonacci(n-1)+fibonacci(n-2)
Пример для версий rakudo-2010.08
Используется рекурсивное определение чисел Фибоначчи. ~ — оператор конкатенации. $_ — переменная по умолчанию, в данном случае счетчик цикла.
sub fibonacci($n) {
$n > 1 or return $n;
return fibonacci($n-1) + fibonacci($n-2);
}
my $st = "";
for 1..16 {
$st ~= fibonacci($_) ~ ", ";
}
say $st, "..."
Пример для версий OpenCOBOL 1.0, TinyCOBOL 0.65.9
Используется итеративное вычисление чисел Фибоначчи. Сложение чисел Фибоначчи выполняется командой ADD, которая суммирует два аргумента и сохраняет результат в третий. Из-за того, что команда DISPLAY делает перевод строки после каждого вызова, найденные числа приходится сохранять в строку-результат, которая выводится уже после цикла. Для конкатенации нового числа с предыдущими используется команда STRING; для каждой переменной из тех, которые объединяются в строку, указывается опция DELIMITED BY: SIZE — используется вся переменная, SPACE — часть переменной до первого пробела. Из-за этого числа выводятся без пробелов после запятых:
001,001,002,003,005,008,013,021,034,055,089,144,233,377,610,987,...
IDENTIFICATION DIVISION.
PROGRAM-ID. SAMPLE.
DATA DIVISION.
WORKING-STORAGE SECTION.
77 fib1 pic 999.
77 fib2 pic 999.
77 fib3 pic 999.
77 i pic 99.
77 fibst pic XXX.
77 res pic X(64).
PROCEDURE DIVISION.
move 0 to i
move 0 to fib1
move 1 to fib2
move "" to res
perform until i greater than 15
add fib1 to fib2 giving fib3
move fib2 to fib1
move fib3 to fib2
move fib1 to fibst
string res DELIMITED BY SPACE
fibst DELIMITED BY SIZE
"," DELIMITED BY SIZE into res
add 1 to i
end-perform.
display res "..."
stop run.
Пример для версий Groovy 1.7
Используется простейшее рекурсивное определение чисел Фибоначчи.
def fib
fib = { n ->
(n <= 2 ? 1 : fib(n-1) + fib(n-2) )
}
(1..16).each { print "${fib(it)}, " }
println "..."
Пример для версий Falcon 0.9.6.6
Используется рекурсивное определение чисел Фибоначчи.
function fib(n)
if n <= 2 : return 1
return fib(n-1) + fib(n-2)
end
for i in [1:17]
print (fib(i), ", ")
end
printl ("...")
Пример для версий Clojure 1.0.0, Clojure 1.1.0
Используется рекурсивное вычисление чисел Фибоначчи.
(defn fibonacci [x]
(if (< x 2)
x
(+ (fibonacci (- x 1)) (fibonacci (- x 2)) )))
(doseq [i (range 1 17)]
(print (str (fibonacci i) ", ")))
(println "...")
Пример для версий guile 1.8.5, JScheme 7.2, MIT/GNU Scheme 7.7.9
Используется рекурсивное определение чисел Фибоначчи.
(define (fibonacci x)
(if (< x 2)
x
(+ (fibonacci (- x 1)) (fibonacci (- x 2)))))
(do ((i 1 (+ i 1)))
((> i 16))
(display (string-append (number->string (fibonacci i)) ", ")))
(display "...")
(newline)
Пример для версий Acme-Chef-1.01
Используется итеративное определение чисел Фибоначчи. Последнее и предпоследнее числа хранятся в переменных fib1 и fib2. За одну итерацию вычисляется следующее число, а предыдущее дописывается в стек и остается в нем для последующего вывода. Второй цикл пересыпает значения во вторую миску в обратном порядке, чтобы на печать они выводились в правильном порядке, по возрастанию.
Данная версия интерпретатора не позволяет работать с символами и числами вперемешку, поэтому формат вывода не соблюдается, и результат работы программы выглядит следующим образом:
1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987
Fibonacci numbers.
This recipe calculates and prints first Fibonacci numbers.
Ingredients.
0 g fib1
1 g fib2
16 g iterator
16 g second iterator
Method.
Chop iterator.
Put fib2 into 1st mixing bowl.
Put fib2 into 1st mixing bowl.
Add fib1 into 1st mixing bowl.
Fold fib2 into 1st mixing bowl.
Fold fib1 into 1st mixing bowl.
Put fib1 into 1st mixing bowl.
Chop iterator until choped.
Mash second iterator.
Fold fib1 into 1st mixing bowl.
Put fib1 into 2nd mixing bowl.
Mash second iterator until mashed.
Pour contents of 2nd mixing bowl into the baking dish.
Serves 1.
Пример для версий Pike 7.6, Pike 7.8
Используется рекурсивное определение чисел Фибоначчи.
int fibonacci(int n) {
return ( n<=2 ? 1 : fibonacci(n-1) + fibonacci(n-2) );
}
int main() {
for (int n=1; n<=16; n++)
write(fibonacci(n)+", ");
write("...\n");
return 0;
}
Пример для версий befungee 0.2.0
Используется итеративное определение чисел Фибоначчи.
В этом примере используются команды p и g, предназначенные для модификации исходного кода программы в процессе выполнения, — они записывают заданный символ в заданную клетку программы и считывают его оттуда в стек, соответственно. В данном случае это используется для хранения вычисленных чисел Фибоначчи (счетчик цикла все время хранится в стеке). При записи чисел как ASCII-кодов символов большие числа искажаются, поэтому выводятся только первые 13 штук.
031p132p 94+ > 31g 32g :. + 32g v
| :-1,,", "p23 p13 <
> "."::,,,25*,@
Пример для версий Morphett's FALSE, Wouter's FALSE 1.2.CF
Используется итеративное вычисление чисел Фибоначчи. Текущие числа хранятся в переменных a и b, счетчик цикла — в i.
Второй цикл примера очищает содержимое стека (числа Фибоначчи, записанные в него первым циклом). Некоторые интерпретаторы позволяют оставлять данные в стеке после конца работы программы, но, к примеру, Wouter’s FALSE 1.2.CF требует, чтобы стек был пустым, и выдает ошибку выполнения в противном случае.
0i: 1a: 1b:
[i;16=~]
[a; $. ", " $ b; $ a: + b: i;1+i:]
#
"..."
[1=~]
[]
#
%
Пример для версий Objeck 2.0.3
Используется рекурсивное определение чисел Фибоначчи.
bundle Default {
class Fib {
function : Fibonacci (n: Int) ~ Int {
if (n<=2) {
return 1;
};
return Fibonacci(n-1) + Fibonacci(n-2);
}
function : Main(args : String[]) ~ Nil {
for (i := 0; i <= 16; i += 1;) {
Fibonacci(i)->Print();
", "->Print();
};
"..."->PrintLine();
}
}
}
Пример для версий Lingua::Shakespeare 1.00
Используется итеративное вычисление чисел Фибоначчи. После выхода из цикла (конец второй сцены) счетчик цикла Isabella используется для вывода троеточия.
use Lingua::Shakespeare;
Fibonacci Numbers.
Isabella, the loop index.
Falstaff, a Fibonacci number.
Fortinbras, another Fibonacci number.
Sebastian, space.
Cordelia, comma.
Act I: Factorial calculations.
Scene I: Initialization.
[Enter Isabella and Sebastian]
Isabella:
You are as fat as the product of a big black furry old cat and a white cow!
[Exit Sebastian]
[Enter Cordelia]
Isabella:
You are as beautiful as the sum of Sebastian and the sum of a tiny yellow furry hamster and the clearest blue sky!
[Exit Cordelia]
[Enter Fortinbras]
Isabella:
You father!
Scene II: Loop.
Isabella:
Open your heart!
You are as noble as the sum of yourself and Falstaff.
[Exit Fortinbras]
[Enter Falstaff]
Isabella:
You are as brave as the difference between Fortinbras and yourself.
[Exit Falstaff]
[Enter Cordelia]
Isabella:
Speak your mind!
[Exit Cordelia]
[Enter Sebastian]
Isabella:
Speak your mind!
[Exit Sebastian]
[Enter Fortinbras]
Fortinbras:
You are as good as the sum of yourself and a rose.
Isabella:
Am I not as beautiful as your sweet charming lovely noble sister?
Fortinbras:
If so, let us return to scene II.
You are as good as the sum of Cordelia and a fine horse!
Speak your mind! Speak your mind! Speak your mind!
[Exeunt]
Пример для версий npiet 1.2
Этот пример сгенерирован автоматически. Ниже приведена исходная программа, из которой он был получен. Используется итеративное вычисление чисел Фибоначчи.
main()
{
f1 = 0;
f2 = 1;
for ( i = 1; i <= 16; i++ )
{
__outn(f2);
__out(44);
__out(32);
f2 = f1 + f2;
f1 = f2 - f1;
}
__out(46);
__out(46);
__out(46);
__out(10);
}

Числа Фибоначчи на Piet
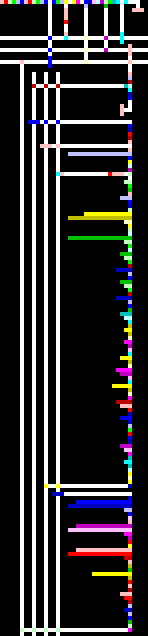
Числа Фибоначчи на Piet (увеличение 4x)
Пример для версий GNU Octave 3.2.3
Используется рекурсивное определение чисел Фибоначчи.
function f = fib(n)
if (n <= 1)
f = n;
else
f = fib(n - 1) + fib(n - 2);
endif
endfunction
for i = 1 : 16
printf("%d, ", fib(i));
endfor
disp("...");
Пример для версий APS APLAN
В языке не предусмотрены операции работы со строками, а команды вывода на печать обязательно заканчивают выведенное переводом строки, поэтому форматирование не соблюдено — числа выводятся просто в столбик.
INCLUDE <include/std.ap>
NAMES fibonacci, print_fibonacci;
fibonacci := rs(x) (
0 = 1,
1 = 1,
x = fibonacci(x - 1) + fibonacci(x - 2)
);
print_fibonacci := proc(n)loc(i, res)(
i := 0;
while(i < n,
prn fibonacci(i);
i := i + 1
)
);
task := print_fibonacci 16 ;
Пример для версий ActiveTcl 8.5, JTcl 2.1.0, Tcl 8.4, Tcl 8.5.7
Используется итеративное определение чисел Фибоначчи.
set fib1 0
set fib2 1
set s ""
for {set i 0} {$i < 16} {incr i} {
set fib3 [expr {$fib1 + $fib2}]
set fib1 $fib2
set fib2 $fib3
append s "$fib1, "
}
puts "$s..."
Пример для версий ActiveTcl 8.5, JTcl 2.1.0, Tcl 8.4, Tcl 8.5.7
Для вычисления чисел используется хвостовая рекурсия. Команда eval позволяет вычислить результат вызова функции fib с заданными аргументами без объявления fib в определенном пространстве имен.
proc fib {f1 f2 n} {
if {$n==0} {
return $f1
} else {
return [eval fib $f2 [expr {$f1 + $f2}] [expr {$n - 1}]]
}
}
set s ""
for {set i 0} {$i < 16} {incr i} {
append s [eval fib 1 1 $i] ", "
}
puts "$s..."
Пример для версий Seed7 2012-01-01
Используется рекурсивное определение чисел Фибоначчи.
$ include "seed7_05.s7i";
const func integer: fibonacci (in var integer: n) is func
result
var integer: result is 1;
begin
if n < 2 then
result := 1;
else
result := fibonacci(n - 1) + fibonacci(n - 2);
end if;
end func;
const proc: main is func
local
var integer: n is 0;
begin
for n range 0 to 15 do
write(fibonacci(n) <& ", ");
end for;
writeln("...");
end func;
Пример для версий Regina 3.3
В этом примере используется рекурсивное определение чисел Фибоначчи.
numbers = ''
do n = 1 to 16
numbers = numbers||fibonacci(n)", "
end
say numbers"..."
exit
fibonacci: procedure
parse arg n .
if n < 3 then
n = 1
else
n = fibonacci(n-1) + fibonacci(n-2)
return n
Пример для версий Regina 3.3
В этом примере используется итеративное вычисление чисел Фибоначчи. Массивы реализованы как “корневые переменные”: обращение к элементам массива идет по их индексам fib.1 (или fib.first).
fib.0 = 0
fib.1 = 1
output = fib.1||', '
do f = 2 to 16
e = f - 1; d = f - 2
fib.f = fib.e + fib.d
output = output||fib.f', '
end
say output"..."
exit
Пример для версий Python 2.6.5
Используется рекурсивное определение чисел Фибоначчи.
def fibonacci(n):
if n < 3:
return 1
else:
return fibonacci(n - 1) + fibonacci(n - 2)
for n in range(1, 16 + 1):
print "%i," % fibonacci(n) ,
print "..."
Пример для версий Rust 0.1
Используется рекурсивное вычисление чисел Фибоначчи.
use std;
import std::io;
fn fibonacci(x: int) -> int {
if (x <= 2) {
ret 1;
} else {
ret fibonacci(x - 1) + fibonacci(x - 2);
}
}
fn main() {
let i = 1;
while i <= 16 {
io::print(#fmt("%d, ", fibonacci(i)));
i = i + 1;
}
io::println("...");
}
Пример для версий Ceylon M1
В этом примере используется итеративное вычисление чисел Фибоначчи.
void run() {
variable String output := "";
variable Integer fib1 := 0;
variable Integer fib2 := 1;
variable Integer fib3;
for (i in 1..16) {
output := "" output "" fib2 ", ";
fib3 := fib1 + fib2;
fib1 := fib2;
fib2 := fib3;
}
print("" output "...");
}
Пример для версий Factor 0.94
В этом примере используется рекурсивное вычисление чисел Фибоначчи. Слово fib вычисляет n-ое число Фибоначчи: если аргумент не больше 1, он остается на стеке в качестве возвращаемого значения, иначе заменяется на сумму предыдущих чисел Фибоначчи. Слово bi является сокращенной формой комбинатора cleave и позволяет применить две цитаты (в данном случае вызовы слова fib для меньших аргументов) к одному элементу стека (n).
USING: formatting kernel math sequences ;
IN: fibonacci-example
: fib ( n -- fib(n) )
dup
1 >
[ [ 1 - fib ] [ 2 - fib ] bi + ]
when ;
16 iota [ 1 + fib "%d, " printf ] each
"...\n" printf
Пример для версий loljs 1.1
Числа Фибоначчи вычисляются итеративно.
HAI
I HAS A I ITS 0
I HAS A FIB1 ITS 0
I HAS A FIB2 ITS 1
IM IN YR LOOP UPPIN YR I TIL BOTH SAEM I AN 16
VISIBLE SMOOSH FIB2 ", "!
I HAS A FIB3 ITS SUM OF FIB1 AN FIB2
FIB1 R FIB2
FIB2 R FIB3
IM OUTTA YR LOOP
VISIBLE "..."
KTHXBYE
Пример для версий loljs 1.1
Числа Фибоначчи вычисляются рекурсивно.
HAI
HOW DUZ I FIBONACCI N
BOTH SAEM 1 AN BIGGR OF N AN 1, O RLY?
YA RLY
FOUND YR 1
NO WAI
FOUND YR SUM OF FIBONACCI DIFF OF N AN 1 AN FIBONACCI DIFF OF N AN 2
OIC
IF U SAY SO
I HAS A N ITZ 0
IM IN YR LOOP UPPIN YR N WILE N SMALLR THAN 16
VISIBLE SMOOSH FIBONACCI N ", "!
IM OUTTA YR LOOP
VISIBLE "..."
KTHXBYE
Пример для версий PostgreSQL 9.1
WITH RECURSIVE t(a,b) AS (
VALUES(1,1)
UNION ALL
SELECT b, a + b FROM t
WHERE b < 1000
)
SELECT array_to_string(array(SELECT a FROM t), ', ') || ', ...';
Пример для версий Dyalog APL 13.1
В этом примере используется формула Бине, реализованная через анонимную динамическую функцию. ⋄ — разделитель выражений, т.е. функция состоит из двух выражений, вычисляющихся слева направо. Первое из них вычисляет золотое сечение и ассоциирует его с именем phi. Второе — вычисляет значение функции через правый аргумент ⍵. ⌈ — округление вверх.
Поскольку функция унарна и определяется через скалярные функции, ее можно применить к массиву, в данном случае к массиву номеров чисел Фибоначчи от 1 до 16, включительно. Результатом будет массив чисел Фибоначчи:
1 1 2 3 5 8 13 21 34 55 89 144 233 377 610 987
{phi←(1+5*0.5)÷2 ⋄ ⌈((phi*⍵) - (1-phi)*⍵)÷5*0.5} 1+⍳16
Пример для версий Dyalog APL 13.1
В данном примере используется анонимно D-функция, рекурсивно вызывающая сама себя. Первое выражение функции обрабатывает случай первых двух чисел Фибоначчи, равных единице. Для остальных чисел работает второе выражение, которое вызывает эту же D-функцию (функция ∇) для меньших значений аргументов и суммирует их. Первая строка ассоциирует массив чисел с переменной fib и ничего не выводит.
Во второй строке вычисленный массив чисел Фибоначчи выводится в нужном формате: к каждому элементу применяется функция, конкатенирующая его с запятой-разделителем, элементы получившегося массива конкатенируются друг с другом (,/) и к результату добавляется троеточие. Итоговый вывод этой команды выглядит следующим образом:
1 , 1 , 2 , 3 , 5 , 8 , 13 , 21 , 34 , 55 , 89 , 144 , 233 , 377 , 610 , 987 , ...
fib←{⍵≤2:1 ⋄ (∇⍵-1)+∇⍵-2}¨1+⍳16
(⊃(,/{⍵, ', '}¨fib)),'...'
Пример для версий g++ 4.x
Используется итеративное вычисление чисел Фибоначчи; вычисленные значения сохраняются в массиве.
#include <iostream>
#include <vector>
using std::cout;
using std::vector;
int main() {
vector<int> fib(17);
fib[0] = 0;
fib[1] = 1;
for (int i = 2; i < 17; ++i) {
fib[i] = fib[i - 2] + fib[i - 1];
}
for (int i = 1; i < 17; ++i) {
cout << fib[i] << ", ";
}
cout << "...\n";
}
Пример для версий Nimrod 0.8.8
Используется итеративное вычисление чисел Фибоначчи. Одним ключевым словом var можно объявить сразу несколько переменных, если эти объявления отформатированы отступами как блок. Тип переменной в объявлении можно не указывать только в том случае, если она инициализируется немедленно; Nimrod использует только локальный вывод типов, не глобальный.
for i in 1..16 — альтернативная форма записи цикла countup. & — оператор конкатенации строк, $ — преобразование числа в строку.
var
f1 = 1
f2 = 1
f3: int
res = ""
for i in 1..16:
res = res & $f1 & ", "
f3 = f1 + f2
f1 = f2
f2 = f3
echo res & "..."
Пример для версий Nimrod 0.8.8
Используется формула Бине. Добавление эпсилона перед округлением необходимо для получения правильных целых значений, т.к. округление выполняется вниз.
from math import sqrt, pow, round
proc fibonacci(n: int): int =
var phi: float64 = (1.0 + sqrt(5.0)) / 2.0
return round((pow(phi, float64(n)) - pow(-phi, -float64(n))) / sqrt(5.0) + 0.0001)
var res = ""
for i in 1..16:
res = res & $fibonacci(i) & ", "
echo res & "..."
Пример для версий VBA 6.3, VBA 6.5
Используется рекурсивное вычисление чисел Фибоначчи. Отметим, что в этом случае тип счетчика цикла i приходятся объявлять в явном виде, иначе он принимает тип Variant и не может быть передан в функцию вместо типа Integer.
Public Function Fibonacci(N As Integer) As Integer
If N < 2 Then
Fibonacci = N
Else
Fibonacci = Fibonacci(N - 1) + Fibonacci(N - 2)
End If
End Function
Sub Fib()
Dim res As String
Dim i As Integer
For i = 1 To 16
res = res & CStr(Fibonacci(i)) & ", "
Next i
MsgBox (res & "...")
End Sub
Пример для версий VBScript 5.7, VBScript 5.8
Числа Фибоначчи вычисляются рекурсивно. Обратите внимание на то, что многие элементы, типичные для Visual Basic, здесь отсутствуют: объявление переменных и типа значения, возвращаемого функцией, явное преобразование чисел в строку для конкатенации и т.д.
Function Fibonacci(N)
If N < 2 Then
Fibonacci = N
Else
Fibonacci = Fibonacci(N - 1) + Fibonacci(N - 2)
End If
End Function
For i = 1 To 16
res = res & Fibonacci(i) & ", "
Next
WScript.Echo (res & "...")
Пример для версий bwBASIC 2.50
Используется итеративное вычисление чисел Фибоначчи с их запоминанием в массиве. Обратите внимание на явное объявление массива и на то, что имя строковой переменной должно заканчиваться на $.
DIM F(16)
F(1) = 1
F(2) = 1
FOR i = 3 TO 16
F(i) = F(i - 1) + F(i - 2)
NEXT i
S$ = ""
FOR i = 1 TO 16
S$ = S$ + STR$(F(i)) + ","
NEXT i
S$ = S$ + " ..."
PRINT S$
Пример для версий X10 Release 2.2.2.2
Рекурсивный метод
import x10.io.Console;
public class Fibonacci {
public static def fib(n:int) {
if (n<=2) return 1;
val f1:int;
val f2:int;
finish {
async { f1 = fib(n-1); }
f2 = fib(n-2);
}
return f1 + f2;
}
public static def main(args:Array[String](1)) {
val n = (args.size > 0) ? int.parse(args(0)) : 10;
Console.OUT.println("Computing fib("+n+")");
val f = fib(n);
Console.OUT.println("fib("+n+") = "+f);
}
}
Пример для версий ECLiPSe CLP 6.0 #188
Числа Фибоначчи вычисляются рекурсивно.
Для организации цикла в предикате main используется специфичная для ECLiPSe итеративная управляющая структура (мета-предикат) for.
fibonacci(1, 1) :- !.
fibonacci(2, 1) :- !.
fibonacci(N, F) :-
N > 2,
N1 is N - 1, N2 is N - 2,
fibonacci(N1, F1), fibonacci(N2, F2),
F is F1 + F2.
main :-
( for(N, 1, 16) do
fibonacci(N, F),
write(F), write(', ') ),
writeln('...').
Пример для версий ECLiPSe CLP 6.0 #188
Числа Фибоначчи вычисляются рекурсивно, при этом используется мемоизация, реализованная при помощи ECLiPSe-специфичного механизма store.
Для организации цикла в предикате main используется специфичная для ECLiPSe итеративная управляющая структура (мета-предикат) for.
:- local store(fibonacci).
fibonacci(1, 1) :- !.
fibonacci(2, 1) :- !.
fibonacci(N, F) :-
N > 2,
(
% используем сохраненный результат
store_get(fibonacci, N, F), !
;
N1 is N - 1, N2 is N - 2,
fibonacci(N1, F1), fibonacci(N2, F2),
F is F1 + F2,
store_set(fibonacci, N, F) % сохраняем полученный результат
).
main :-
( for(N, 1, 16) do
fibonacci(N, F),
write(F), write(', ') ),
writeln('...').
Пример для версий A++ Interpreter
В этом примере используется хвостовая рекурсия.
(load "app/init.app")
(define fibonacci (lambda(f1 f2 n)
(if (equal n 0)
f1
(fibonacci f2 (+ f1 f2) (- n 1)))
))
(define main
(lambda(n)
(while (not (equal n 16))
(lambda()
(print (fibonacci 1 1 n))
(define n (+ n 1))))))
(main 0)
Пример для версий f2c 20090411, g95 0.93, gfortran 4.5.0
Этот пример демонстрирует использование массивов в Fortran. Индексация элементов начинается с 1.
PROGRAM FIBONACCI
INTEGER FIB(20)
FIB(1) = 0
FIB(2) = 1
DO 1,N = 2,17
PRINT "(I3, A, $)", FIB(N), ", "
1 FIB(N + 1) = FIB(N) + FIB(N - 1)
PRINT *, "..."
END
Пример для версий R 2.10.1
Используется рекурсивное вычисление чисел Фибоначчи. Функция создается как объект и присваивается переменной fib. Если функция return не вызывается в явном виде, функция возвращает значение последней выполненной команды.
Функция print.table выводит массив, полученный в результате применения функции fib к массиву чисел от 1 до 16, как таблицу, т.е. в одну строку. Использование функции print вывело бы элементы массива по одному на строку.
fib <- function(n) {
if (n < 2)
n
else
fib(n - 1) + fib(n - 2)
}
print.table(lapply(1:16, fib))
Пример для версий MIPS32
Эмулятор MARS. Вывод консоли MARS:
The Fibonacci numbers are:
1 1 2 3 5 8 13 21 34 55 89 144
-- program is finished running --
Программа выводит 15 чисел Фибоначчи. Количество чисел можно изменить в секции .data.
.data
space:.asciiz " "
head: .asciiz "The Fibonacci numbers are:\n"
fib: .word 0 : 15
size: .word 15
.text
main:
la $t0, fib
la $t5, size
lw $t5, 0($t5)
li $t2, 1
add.d $f0, $f2, $f4
sw $t2, 0($t0)
sw $t2, 4($t0)
addi $t1, $t5, -2
loop:
lw $t3, 0($t0)
lw $t4, 4($t0)
add $t2, $t3, $t4
sw $t2, 8($t0)
addi $t0, $t0, 4
addi $t1, $t1, -1
bgtz $t1, loop
la $a0, fib
move $a1, $t5
jal print
li $v0, 10
syscall
print:
add $t0, $zero, $a0
add $t1, $zero, $a1
la $a0, head
li $v0, 4
syscall
out:
lw $a0, 0($t0)
li $v0, 1
syscall
la $a0, space
li $v0, 4
syscall
addi $t0, $t0, 4
addi $t1, $t1, -1
bgtz $t1, out
jr $ra
Пример для версий E-on-Java 0.9.3
var s := [0, 1]
var res := ""
for _ in 1..16 {
def [a, b] := s
s := [b, a + b]
res := res + b.toString(10) + ", "
}
println(res + "...")
Пример для версий Mathics 0.4
Этот пример использует функцию Riffle, которая в данном случае перемежает элементы массива чисел Фибоначчи копиями строки “,”.
StringJoin[Riffle[Map[ToString, Table[Fibonacci[i], {i,16}]], ", "]] <> "..."
Пример для версий Dart 1.1.1
Используется рекурсивное определение чисел Фибоначчи.
int fibonacci(int n) => n <= 2 ? 1 : fibonacci(n - 2) + fibonacci (n - 1);
main() {
String output = "";
for (int i = 1; i <= 16; ++i) {
output += fibonacci(i).toString() + ", ";
}
print(output + "...");
}
Пример для версий Snap! 4.0
Этот пример реализует рекурсивное вычисление чисел Фибоначчи. Для ускорения работы программы ранее найденные числа записываются в “кэш” — глобальный список.
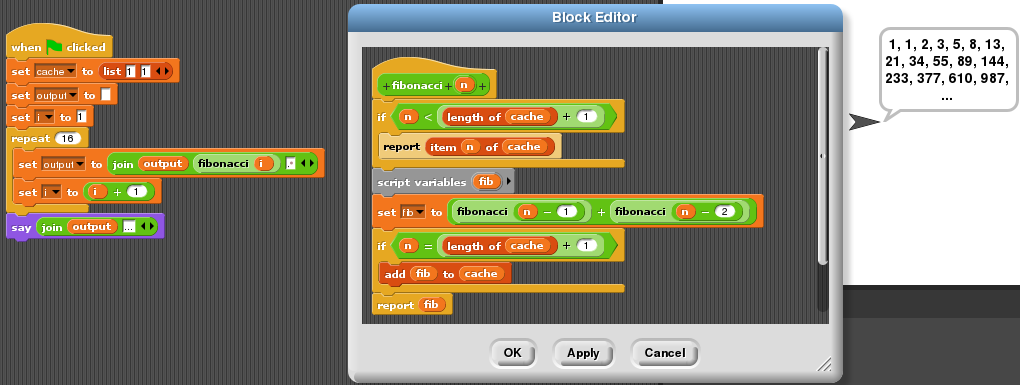
Числа Фибоначчи (рекурсивное вычисление) на Snap!
Пример для версий Rust 1.0.0-alpha.2
fn fibonacci(x: i64) -> i64 {
if x <= 2 {
1
} else {
fibonacci(x - 1) + fibonacci(x - 2)
}
}
fn main() {
for i in 1..17 {
print!("{}, ", fibonacci(i));
}
println!("...");
}
Пример для версий Vala 0.30
void fibonacci(){
long output = 1;
while(true){
print(@"$output \n");
output += output;
}
}
Пример для версий Windows PowerShell 5.0
function Get-Fibonacci ($n) {
if ($n -le 1) {
return 1
}
return (Get-Fibonacci ($n - 1)) + (Get-Fibonacci ($n - 2))
}
$output = ""
foreach ($i in 0..15) {
$output += ("{0}, " -f (Get-Fibonacci $i))
}
echo "$output..."
Пример для версий Microsoft SQL Server 2005, Microsoft SQL Server 2008 R2, Microsoft SQL Server 2012
Используется возможность рекурсивных запросов. Кол-во членов ряда — 92
declare @max_n tinyint = 92
;with t as (
select n = 1, fib = convert(bigint,1), xfib = convert(bigint,0)
union all
select n = n+1, fib = fib+xfib, xfib = fib from t
where n < @max_n
)
select fib from t
Пример для версий Clarion C10
использование 64-битной арифметики
PROGRAM
OMIT('***')
* User: Shur
* Date: 29.02.2016
* Time: 21:18
***
MAP
include('i64.inc')
ShowINT64 PROCEDURE(*INT64 a),STRING
END
a LIKE(INT64)
b LIKE(INT64)
c LIKE(INT64)
str1 CSTRING(32000)
str2 CSTRING(32000)
CODE
a.lo = 1
str1 = '1=' & ShowINT64(a)
b.lo = 1
str1 = str1 & '|2=' & ShowINT64(b)
str2 ='1, 1'
loop i# = 3 to 200
i64Add(a,b,c)
if i64Sign(c) = -1
break
end
a :=: b ! deep assignment uses for structures
b = c ! usual assignment can be also used
str1 = str1 & '|' & i# & '=' & ShowINT64(c)
str2 = str2 & ', ' & ShowINT64(c)
end
message(str2,'Fibonacci',,,,10b)
message(str1,'Fibonacci',,,,10b)
ShowINT64 PROCEDURE(a)
d DECIMAL(30,0)
CODE
i64ToDecimal(d,a)
return(d)