Квадратное уравнение
Квадратное уравнение — это уравнение вида Ax2 + Bx + C = 0, где A, B и C — заданные константы (с ограничением A != 0).
Первым шагом решения уравнения является вычисление дискриминанта D = B2-4AC. Если D = 0, уравнение имеет единственный действительный корень x = -B/2A, в противном случае существует пара корней x1 = (-B+sqrt(D))/2A, x2 = (-B-sqrt(D))/2A (корни являются действительными или комплексными в зависимости от знака дискриминанта).
Примеры:
-
x + 1 = 0— не квадратное уравнение; -
x2 — 2x + 1 = 0— единственный корень1; -
x2 — 1 = 0— пара корней1и-1; -
2x2 — 3x + 1 = 0— пара корней1и0.5; -
x2 + 1 = 0— пара комплексных корнейiи-i(или(0, 1)и(0, -1)).
Задача состоит в том, чтобы прочитать целочисленные константы A, B и C, заданные пользователем, вычислить корни уравнения и вывести их. Если A = 0, выведите сообщение об ошибке “Уравнение не является квадратным” (“Not a quadratic equation.”). Корни следует выводить в формате (a, b) или a + ib, где a и b — дробные числа с 6 или менее знаками после десятичной запятой.
Этот класс примеров демонстрирует работу с дробными и комплексными числами (если язык предоставляет эти типы данных), а также с математическими функциями. Кроме того, для общения с пользователем может использоваться как консоль, так и графический интерфейс.
Пример для версий Borland C++ Builder 6, g++ 3.4.5, Microsoft Visual C++ 9 (2008)
В этом примере используется класс complex<>, входящий в состав библиотеки STL. Все вычисления выполняются в комплексных числах, т.к. это позволяет не беспокоиться о знаке дискриминанта и различных представлениях корней для действительного и комплексного случаев.
Оператор >> класса complex<> перегружен так, что он распознает несколько форматов вводимых чисел, в т.ч. и числа без мнимой части, так что константы A, B и C читаются не как целые числа, а сразу как комплексные. Такая реализация позволяет расширить область применения примера до уравнений с дробными и даже комплексными коэффициентами.
Оператор << класса complex<> также перегружен и выводит любое комплексное число x как (x.real(),x.imag()), поэтому для вывода корней без мнимой части как обычных дробных чисел используется функция print.
#include <iostream>
#include <complex>
#include <math>
using namespace std;
void print(int ind, complex<double> x)
{ cout << "x" << ind << " = ";
if (fabs(x.imag()) < 1E-6)
cout << x.real() << endl;
else cout << x << endl;
}
void main()
{ complex<double> A, B, C, D, x1, x2;
cout << "A = ";
cin >> A;
if (abs(A)<1E-3)
{ cout << "Not a quadratic equation." << endl;
return;
}
cout << "B = ";
cin >> B;
cout << "C = ";
cin >> C;
A *= 2;
D = B*B-A*C*2.0;
if (abs(D)<1E-3)
cout << "x = " << (-B/A).real();
else
{ print(1, (-B+sqrt(D))/A);
print(2, (-B-sqrt(D))/A);
}
}
Пример для версий SpiderMonkey (Firefox 3.5)
Пример выполняется в веб-браузере. Чтобы запустить пример, скопируйте код в файл quadratic.js и создайте файл HTML, находящийся в том же каталоге, содержащий следующий текст:
<head>
<script type="text/javascript" src="quadratic.js"></script>
</head>
<body>
<form name="quadratic">
<input type="number" required="required" name="A">
<input type="number" required="required" name="B">
<input type="number" required="required" name="C">
<input type="button" value="Solve" onClick="solve()">
</form>
<p id="output">
</p>
</body>
Это создаст веб-страницу с тремя полями ввода и кнопкой. При нажатии на кнопку будет решено уравнение с введенными коэффициентами, и корни будут напечатаны под полями ввода.
В JavaScript нет типа данных для работы с комплексными числами, поэтому вычисления производятся в дробных числах и выполняется отдельная проверка на знак дискриминанта. Реализация позволяет решать квадратные уравнения не только с целыми, но и с дробными коэффициентами.
function print(real, imag)
{ if (Math.abs(imag)<1E-6)
return real;
else
return '('+real+','+imag+')';
}
function solve()
{ A = document.quadratic.A.value;
if (Math.abs(A)<1E-3)
{ document.getElementById('output').innerHTML = 'Not a quadratic equation.';
return;
}
B = document.quadratic.B.value;
C = document.quadratic.C.value;
A = 2*A;
D = B*B-2*A*C;
if (Math.abs(D)<1E-3)
{ document.getElementById('output').innerHTML = 'x = '+(-B/A);
return;
}
if (D>0)
document.getElementById('output').innerHTML = 'x1 = '+print((-B+Math.sqrt(D))/A, 0)+'<br />x2 = '+print((-B-Math.sqrt(D))/A, 0);
else
document.getElementById('output').innerHTML = 'x1 = '+print(-B/A,Math.sqrt(-D)/A)+'<br />x2 = '+print(-B/A,-Math.sqrt(-D)/A);
}
Пример для версий gcj 3.4.5, Groovy 1.7, Sun Java 6
В Java нет типа данных для работы с комплексными числами, поэтому вычисления производятся в дробных числах и выполняется отдельная проверка на знак дискриминанта. Реализация позволяет решать квадратные уравнения не только с целыми, но и с дробными коэффициентами.
Коэффициенты читаются из потока System.in. Напрямую из него можно читать только отдельные байты, поэтому для повышения комфортности чтения используются классы InputStreamReader и BufferedReader. Строки, прочитанные из System.in, преобразуются в числа типа double с помощью метода Double.parseDouble(). Все операции ввода в Java должны находиться внутри блоков try ... catch, чтобы гарантированно обрабатывать IOException — класс исключений, порождаемых функциями чтения.
import java.util.*;
import java.io.*;
public class Quadratic {
static String print(double real, double imag)
{ if (Math.abs(imag)<1E-6)
return ""+real;
else
return "("+real+","+imag+")";
}
public static void main(String[] args)
{ double A,B,C,D;
try {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
System.out.print("A = ");
A = Double.parseDouble(br.readLine());
if (Math.abs(A)<1E-3)
{ System.out.println("Not a quadratic equation.");
return;
}
System.out.print("B = ");
B = Double.parseDouble(br.readLine());
System.out.print("C = ");
C = Double.parseDouble(br.readLine());
}
catch (Exception e) {
System.err.println("An error occured while reading input parameters.");
return;
}
A = 2*A;
D = B*B-2*A*C;
if (Math.abs(D)<1E-3)
{ System.out.println("x = "+(-B/A));
return;
}
if (D>0)
System.out.println("x1 = "+print((-B+Math.sqrt(D))/A, 0)+"\nx2 = "+print((-B-Math.sqrt(D))/A, 0));
else
System.out.println("x1 = "+print(-B/A,Math.sqrt(-D)/A)+"\nx2 = "+print(-B/A,-Math.sqrt(-D)/A));
}
}
Пример для версий Oracle 10g SQL, Oracle 11g SQL
Этот пример тестировался в SQL*Plus, TOAD и PL/SQL Developer.
Чистый SQL позволяет вводить переменные в процессе исполнения запроса в виде заменяемых переменных. Для определения такой переменной ее имя (в данном случае A, B и C) следует использовать с амперсандом & перед ним каждый раз, когда нужно сослаться на эту переменную. Когда запрос выполняется, пользователь получает запрос на ввод значений всех заменяемых переменных, использованных в запросе. После ввода значений каждая ссылка на такую переменную заменяется на ее значение, и полученный запрос выполняется.
Существует несколько способов ввести значения для заменяемых переменных. В данном примере первая ссылка на каждую переменную предваряется не одинарным, а двойным амперсандом &&. Таким образом значение для каждой переменной вводится только один раз, а все последующие ссылки на нее будут заменены тем же самым значением (при использовании одиночного амперсанда в SQL*Plus значение для каждой ссылки на одну и ту же переменную приходится вводить отдельно). В PL/SQL Developer ссылки на все переменные должны предваряться одиночным знаком &, иначе будет возникать ошибка ORA-01008 “Not all variables bound”.
Следует отметить, что ссылки заменяются на значения “как есть”, поэтому отрицательные коэффициенты следует вводить в скобках.
Первая строка примера задает символ для десятичного разделителя, который используется при преобразовании чисел-корней в строки.
Сам запрос состоит из четырех разных запросов. Каждый запрос возвращает строку, содержащую результат вычислений, в одном из случаев (A=0, D=0, D>0 и D<0) и ничего — в трех остальных случаях. Результаты всех четырех запросов объединяются, чтобы получить окончательный результат.
alter session set NLS_NUMERIC_CHARACTERS='. ';
select 'Not a quadratic equation.' ans
from dual
where &&A = 0
union
select 'x = ' || to_char(-&&B/2/&A)
from dual
where &A != 0 and &B*&B-4*&A*&&C = 0
union
select 'x1 = ' || to_char((-&B+sqrt(&B*&B-4*&A*&C))/2/&A) || ', x2 = ' || to_char(-&B-sqrt(&B*&B-4*&A*&C))/2/&A
from dual
where &A != 0 and &B*&B-4*&A*&C > 0
union
select 'x1 = (' || to_char(-&B/2/&A) || ',' || to_char(sqrt(-&B*&B+4*&A*&C)/2/&A) || '), ' ||
'x2 = (' || to_char(-&B/2/&A) || ',' || to_char(-sqrt(-&B*&B+4*&A*&C)/2/&A) || ')'
from dual
where &A != 0 and &B*&B-4*&A*&C < 0;
Пример для версий UCBLogo 6.0
В этом примере определяется функция, принимающая в качестве аргументов коэффициенты квадратного уравнения и выводящая на печать его корни.
to quadratic :A :B :C
if :A = 0 [(print [Not a quadratic equation.])
stop
]
make "D :B*:B - 4*:A*:C
if :D = 0 [(print [x = ] -:B/2/:A)
stop
]
if :D > 0 [(print [x1 = ] (-:B+sqrt :D)/2/:A)
(print [x2 = ] (-:B-sqrt :D)/2/:A)
stop
]
(print [x1 = (] -:B/2/:A [,] (sqrt (-:D))/2/A [)])
(print [x2 = (] -:B/2/:A [,] (-sqrt (-:D))/2/A [)])
end
Пример для версий clisp 2.47, Corman Common Lisp 3.0, gcl 2.6.6, SBCL 1.0.1, SBCL 1.0.29
Common Lisp позволяет работать с комплексными числами и выводить их на печать в формате #C(real imag). Функция write-to-string преобразует число в строку.
(defun quadratic-roots-2 (A B C)
(cond ((= A 0) (string "Not a quadratic equation."))
(t
(let ((D (- (* B B) (* 4 A C))))
(cond ((= D 0) (concatenate 'string "x = " (write-to-string (/ (+ (- B) (sqrt D)) (* 2 A)))))
(t
(concatenate 'string (concatenate 'string "x1 = " (write-to-string (/ (+ (- B) (sqrt D)) (* 2 A))))
(concatenate 'string "~%x2 = " (write-to-string (/ (- (- B) (sqrt D)) (* 2 A)))))))))))
(let ((A (read))
(B (read))
(C (read)))
(format t (quadratic-roots-2 A B C)))
Пример для версий gnat 3.4.5
Ada предоставляет тип данных для работы с комплексными числами, который требует использования пакетов Generic_Complex_Types и Generic_Complex_Elementary_Functions с предварительной инициализацией их типом данных для хранения комплексных чисел (в данном случае — Float). Ada не поддерживает неявные преобразования типов, поэтому все преобразования выполняются в явном виде.
with Ada.Text_IO,
Ada.Integer_Text_IO,
Ada.Float_Text_IO,
Ada.Numerics.Elementary_Functions,
Ada.Text_IO.Complex_IO,
Ada.Numerics.Generic_Complex_Types,
Ada.Numerics.Generic_Complex_Elementary_Functions;
use Ada.Text_IO, Ada.Integer_Text_IO, Ada.Float_Text_IO;
procedure QuadraticEquation is
package Complex_Types is new Ada.Numerics.Generic_Complex_Types (Float);
package Complex_Functions is new Ada.Numerics.Generic_Complex_Elementary_Functions(Complex_Types);
package Complex_IO is new Ada.Text_IO.Complex_IO (Complex_Types);
use Complex_Types, Complex_Functions, Complex_IO;
A,B,C,D: Integer;
A2f, Bf, S: Float;
Dc: Complex;
begin
Put("A = ");
Get(Item => A);
if A = 0 then
Put_Line("Not a quadratic equation.");
return;
end if;
Put("B = ");
Get(B);
Put("C = ");
Get(C);
A2f := Float(2*A);
Bf := Float(B);
D := B*B-4*A*C;
if D = 0 then
Put("x = ");
Put(-Bf/A2f);
elsif D > 0 then
S := Ada.Numerics.Elementary_Functions.Sqrt(Float(D));
Put("x1 = ");
Put((-Bf+S)/A2f);
Put_Line("");
Put("x2 = ");
Put((-Bf-S)/A2f);
else
Dc := Compose_From_Cartesian (Re => Float(D), Im => 0.0);
Put("x1 = ");
Put((-Bf+Complex_Functions.Sqrt(Dc))/A2f);
Put_Line("");
Put("x2 = ");
Put((-Bf-Complex_Functions.Sqrt(Dc))/A2f);
end if;
end QuadraticEquation;
Пример для версий GHC 6.10.4
Haskell предоставляет тип данных для работы с комплексными числами. Функция quadratic принимает в качестве аргумента список трех комплексных чисел (коэффициентов уравнения) и возвращает список корней уравнения. Запись вида root sign позволяет передать знак операции в качестве аргумента и таким образом обобщить запись двух знаков при квадратном корне из дискриминанта.
module Main where
import Data.Complex
import System.IO (hFlush, stdout)
quadratic :: (Complex Double, Complex Double, Complex Double) -> [Complex Double]
quadratic (0, _, _) = []
quadratic (a, b, c)
| d == 0 = [root (+)]
| otherwise = [root (+), root (-)]
where d = b*b - 4*a*c
root sign = sign (-b) (sqrt d) / (2*a)
main = do
putStr "A = "
hFlush stdout
a <- readLn :: IO Double
putStr "B = "
hFlush stdout
b <- readLn :: IO Double
putStr "C = "
hFlush stdout
c <- readLn :: IO Double
print $ quadratic (realToFrac a, realToFrac b, realToFrac c)
Пример для версий Visual Prolog 7.2
Для запуска создайте новый проект с UI Strategy “Console” и замените содержимое файлов main.cl и main.pro приведенным кодом.
В main.cl добавлена одна строка q : () procedure().. Ключевое слово procedure описывает поведение предиката, указывая, что его вычисление всегда будет успешным и будет найдено ровно одно решение, так что откаты не понадобятся.
В main.pro находится собственно определение нового предиката. Предикат q не принимает аргументов, поскольку читает необходимые данные из stdio. Условное оценивание (конструкцияif-then-else) работает точно так же, как в других языках. Единственным отличием является знак отсечения ! перед then. Это означает, что как только условие if выполняется, откат уже не потребуется.
Хитрость этого примера в том, что невозможно сразу вычислить дискриминант, как в других языках. Тип данных по умолчанию для переменной D в присвоении D = B*B-4*A*C -uReal, который может хранить только неотрицательные числа.
% main.cl
class main
open core
predicates
classInfo : core::classInfo.
q : () procedure().
predicates
run : core::runnable.
end class main
% main.pro
implement main
open core
constants
className = "main".
classVersion = "".
clauses
classInfo(className, classVersion).
q() :-
stdio::write("A = "),
A = stdio::read(),
if (A = 0), ! then
stdio::write("Not a quadratic equation."), stdio::nl
else
stdio::write("B = "),
B = stdio::read(),
stdio::write("C = "),
C = stdio::read(),
if (B*B = 4*A*C), ! then
stdio::writef("x = %f", -B/2.0/A)
elseif (B*B > 4*A*C), ! then
D = B*B-4*A*C,
stdio::writef("x1 = %f\n", (-B+math::sqrt(D))/2.0/A),
stdio::writef("x2 = %f", (-B-math::sqrt(D))/2.0/A)
else
D = -B*B+4*A*C,
stdio::writef("x1 = (%f, %f)\n", -B/2.0/A, math::sqrt(D)/2.0/A),
stdio::writef("x2 = (%f, %f)", -B/2.0/A, -math::sqrt(D)/2.0/A)
end if
end if.
clauses
run():-
console::init(),
q(),
succeed().
end implement main
goal
mainExe::run(main::run).
Пример для версий Free Pascal 2.2.0, gpc 20070904, PascalABC.NET 1.8, Turbo Pascal 1.0, Turbo Pascal 2.0, Turbo Pascal 3.0, Turbo Pascal 4.0, Turbo Pascal 5.0, Turbo Pascal 6.0
В Pascal есть встроенный комплексный тип данных complex, но команда writeln не работает с ним напрямую (только через функции Re и Im), поэтому существенного удобства от его использования нет. Вычисления проводятся в типе real. Библиотечная функция halt, введенная в Extended Pascal, позволяет выйти из текущего блока (в более поздних версиях заменена на exit).
program Quadratic;
var
A,B,C,D: integer;
begin
write('A = ');
readln(A);
if (A=0) then
begin
writeln('Not a quadratic equation.');
halt;
end;
write('B = ');
readln(B);
write('C = ');
readln(C);
D := B*B-4*A*C;
if (D=0) then
begin
writeln('x = ',-B/2.0/A);
halt;
end;
if (D>0) then
begin
writeln('x1 = ',(-B+Sqrt(D))/2.0/A);
writeln('x2 = ',(-B-Sqrt(D))/2.0/A);
end
else
begin
writeln('x1 = (',-B/2.0/A,',',Sqrt(-D)/2.0/A,')');
writeln('x2 = (',-B/2.0/A,',',-Sqrt(-D)/2.0/A,')');
end;
end.
Пример для версий QuickBasic 4.50
PRINT "A = "
INPUT A
IF (A = 0) THEN
PRINT "Not a quadratic equation."
ELSE
PRINT "B = "
INPUT B
PRINT "C = "
INPUT C
D = B * B - 4 * A * C
IF (D = 0) THEN
PRINT "x = " + STR$(-B / 2! / A)
ELSE
IF (D > 0) THEN
PRINT "x1 = " + STR$((-B + SQR(D)) / 2! / A)
PRINT "x2 = " + STR$((-B - SQR(D)) / 2! / A)
ELSE
PRINT "x1 = (" + STR$(-B / 2! / A) + "," + STR$(SQR(-D) / 2! / A) + ")"
PRINT "x2 = (" + STR$(-B / 2! / A) + "," + STR$(-SQR(-D) / 2! / A) + ")"
END IF
END IF
END IF
Пример для версий Wolfram Mathematica 7.0.1.0, Wolfram Mathematica 8.0.4
После ввода коэффициентов определяем переменную y — квадратное уравнение с заданными коэффициентами. Так как x не определено, в уравнении оно останется обычной переменной (например, Print[y] выведет запись полученного уравнений c + b x + a x^2 с подставленными коэффициентами a, b и c). Функция Reduce вычисляет значения переменных, при котором указанное условие будет истинным. Условие в данном случае — квадратное уравнение, а переменная — x.
a = Input["Input a", 0];
b = Input["Input b", 0];
c = Input["Input c", 0];
y = a*x^2 + b*x + c;
Print[Reduce[y == 0]];
Пример для версий Euphoria 3.1.1
include get.e
atom A
atom B, C
atom D
A = prompt_number("A=", {})
if A = 0 then
puts(1,"Not a quadratic equation.\n")
else
B = prompt_number("B=", {})
C = prompt_number("C=", {})
D = B*B - 4*A*C
if D = 0 then
printf(1,"x = %g\n", -B/2/A)
else
if D > 0 then
printf(1,"x1 = %g\n", -B+sqrt(D)/2/A)
printf(1,"x2 = %g\n", -B-sqrt(D)/2/A)
else
printf(1,"x1 = (%g,%g)\n", {-B/2/A, sqrt(-D)/2/A})
printf(1,"x2 = (%g,%g)\n", {-B/2/A, sqrt(-D)/2/A})
end if
end if
end if
Пример для версий VB.NET 9 (2008), vbnc 2.4.2
Module Module1
Sub Main()
Dim A, B, C, D As Integer
Dim p1, p2 As Double
Try
Console.Write("A = ")
A = Val(Console.ReadLine())
Console.Write("B = ")
B = Val(Console.ReadLine())
Console.Write("C = ")
C = Val(Console.ReadLine())
Catch ex As Exception
Console.WriteLine("Invalid input.")
Return
End Try
If A = 0 Then
Console.WriteLine("Not a quadratic equation.")
Return
End If
D = B * B - 4 * A * C
p1 = -B / 2.0 / A
p2 = Math.Sqrt(Math.Abs(D)) / 2.0 / A
If D = 0 Then
Console.Write("x = " & p1.ToString())
ElseIf D > 0 Then
Console.WriteLine("x1 = " & (p1 + p2).ToString())
Console.WriteLine("x2 = " & (p1 - p2).ToString())
Else
Console.WriteLine("x1 = (" & p1.ToString() & "," & p2.ToString() & ")")
Console.WriteLine("x2 = (" & p1.ToString() & ",-" & p2.ToString() & ")")
End If
End Sub
End Module
Пример для версий gawk 3.1.6, Jawk 1.02, mawk 1.3.3
{ A = $1
B = $2
C = $3
if (A == 0)
print "Not a quadratic equation"
else
{ D = B*B-4*A*C
if (D == 0)
print "x = " (-B/2/A)
else if (D > 0)
{ print "x1 = " ((-B+sqrt(D))/2/A)
print "x2 = " ((-B-sqrt(D))/2/A)
}
else
{ print "x1 = (" (-B/2/A) "," (sqrt(-D)/2/A) ")"
print "x2 = (" (-B/2/A) "," (-sqrt(-D)/2/A) ")"
}
}
}
Пример для версий erl 5.7.3
-module(prog).
-export([main/0]).
solve(A, B, C) ->
D = B*B - 4*A*C,
if (D == 0) -> io:format("x = ~f~n", [-B*0.5/A]);
true ->
if (D > 0) ->
SQ = math:sqrt(D),
io:format("x1 = ~f~nx2 = ~f", [(-B+SQ)/2/A, (-B-SQ)/2/A]);
true -> SQ = math:sqrt(-D),
io:format("x1 = (~f,~f)~nx2 = (~f,~f)", [-0.5*B/A, 0.5*SQ/A, -0.5*B/A, -0.5*SQ/A])
end
end
.
main() ->
case io:fread("A = ", "~d") of
eof -> true;
{ok, X} ->
[A] = X,
if (A == 0) -> io:format("Not a quadratic equation.");
true ->
case io: fread("B = ", "~d") of
eof -> true;
{ok, Y} ->
[B] = Y,
case io: fread("C = ", "~d") of
eof -> true;
{ok, Z} ->
[C] = Z,
solve(A, B, C)
end
end
end
end.
Пример для версий GDC 0.24
import std.c.stdio;
import std.stdio;
import std.math;
int main() {
int A, B, C;
writef("A = ");
scanf("%d", & A);
if (A==0)
{ writefln("Not a quadratic equation.");
return 0;
}
writef("B = ");
scanf("%d", & B);
writef("C = ");
scanf("%d", & C);
A*=2;
float D = B*B-2*A*C;
if (D == 0)
{ writefln("x = %f\n",-B*1.0/A);
return 0;
}
if (D>0)
writefln("x1 = %f\nx2 = %f",(-B+sqrt(D))/A,(-B-sqrt(D))/A);
else
writefln("x1 = (%f, %f)\nx2 = (%f, %f)",-B*1.0/A,sqrt(-D)/A,-B*1.0/A,-sqrt(-D)/A);
return 0;
}
Пример для версий gmcs 2.0.1
using System;
class Program
{
static void Main(string[] args)
{
int A, B, C, D;
try
{ Console.Write("A = ");
A = Convert.ToInt32(Console.ReadLine());
Console.Write("B = ");
B = Convert.ToInt32(Console.ReadLine());
Console.Write("C = ");
C = Convert.ToInt32(Console.ReadLine());
}
catch
{ Console.WriteLine("Invalid input");
return;
}
if (A == 0)
{ Console.WriteLine("Not a quadratic equation.");
return;
}
D = B * B - 4 * A * C;
if (D == 0)
Console.WriteLine("x = {0}", -B / 2.0 / A);
else if (D > 0)
Console.WriteLine("x1 = {0}\nx2 = {1}", (-B + Math.Sqrt(D)) / 2 / A, (-B - Math.Sqrt(D)) / 2 / A);
else
Console.WriteLine("x1 = ({0},{1})\nx2 = ({0},-{1})", -B/2.0/A, Math.Sqrt(-D)/2/A);
}
}
Пример для версий Scala 2.8.0-final
Из этого примера видно, что многие вещи — математика, обработка ввода, работа со строками — в Scala заимствована из Java.
import java.io.{BufferedReader, InputStreamReader}
object Main {
def main(args: Array[String]) {
var stdin = new BufferedReader(new InputStreamReader(System.in));
var A = augmentString(stdin.readLine()).toInt;
var B = augmentString(stdin.readLine()).toInt;
var C = augmentString(stdin.readLine()).toInt;
solve(A,B,C);
}
def output(real: Double, imag: Double): String =
if (imag == 0) ""+real
else "("+real+","+imag+")"
def solve(A: Int, B: Int, C: Int)
{ if (A == 0) print("Not a quadratic equation.")
else
{ def D = B*B - 4*A*C;
if (D == 0) print("x = "+output(-B/2.0/A, 0));
else if (D > 0)
print("x1 = "+output((-B+Math.sqrt(D))/2.0/A, 0)+"\nx2 = "+output((-B-Math.sqrt(D))/2.0/A, 0));
else print("x1 = "+output(-B/2/A, Math.sqrt(-D)/2.0/A)+"\nx2 = "+output(-B/2/A, -Math.sqrt(-D)/2.0/A));
}
}
}
Пример для версий Borland C++ Builder 6, g++ 3.4.5, gcc 3.4.5, gcc 3.4.5 (Objective-C), Microsoft Visual C++ 9 (2008), TCC 0.9.25
Этот пример работает на C и C++, а также на Objective-C, являющемся строгим надмножеством языка C. В случае C может понадобиться компилировать программу с опцией -lm, чтобы подключить библиотеку математики.
#include <math.h>
#include <stdio.h>
int main()
{
int A, B, C, D;
printf("A = ");
scanf("%d", &A);
if (A == 0) {
printf("Not a quadratic equation.\n");
return 0;
}
printf("B = ");
scanf("%d", &B);
printf("C = ");
scanf("%d", &C);
D = B * B - 4 * A * C;
if (D == 0) {
printf("x = %f\n", -B / 2.0 / A);
return 0;
}
if (D > 0) {
printf("x1 = %f\nx2 = %f\n",
(-B + sqrt(D)) / 2.0 / A, (-B - sqrt(D))/ 2.0 / A);
} else {
printf("x1 = (%f, %f)\nx2 = (%f, %f)\n",
-B / 2.0 / A, sqrt(-D) / 2.0 / A, -B / 2.0 / A, -sqrt(-D) / 2.0 /A);
}
return 0;
}
Пример для версий Scratch 1.4
Этот пример демонстрирует использование ввода пользовательских данных в Scratch командой ask "..." and wait. В результате этой команды спрайт “говорит” заданное сообщение (приглашение к вводу), и под спрайтом показывается окно ввода. Когда информация введена, ее можно получить через предопределенную переменную answer. При вводе нескольких значений подряд каждое из них следует скопировать в локальную переменную, прежде чем переходить ко вводу следующего.
ask "A = ?" and wait
set A to answer
if A = 0
say "Not a quadratic equation"
else
ask "B = ?" and wait
set B to answer
ask "C = ?" and wait
set C to answer
set D to B*B + (-4)*A*C
set re to B/(-2*A)
if D = 0
say join ("x = " re)
else
set im to (sqrt of (abs of D)) / (2*A)
if D > 0
say join (join ("x1 = " (re+im)) join (", x2 = " (re-im)))
else
say join (join ("x1 = (" join (re join (", " im))) join ("), x2 = (" join (re join (", -" join (im ")")))))
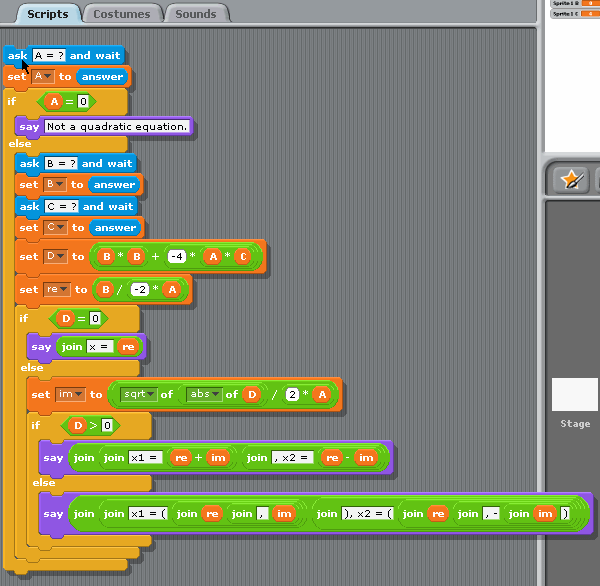
Квадратное уравнение на Scratch
Пример для версий Sanscript 2.2
Этот пример содержит много условных переходов, а в Sanscript каждая ветвь описывается отдельной диаграммой.
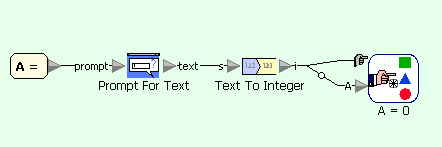
Квадратное уравнение - главная диаграмма потоков
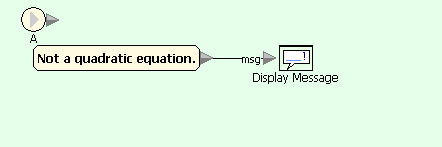
Квадратное уравнение - условие A=0
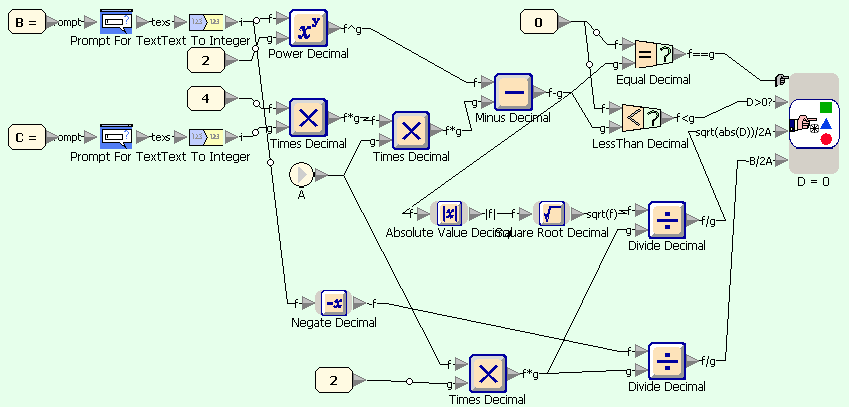
Квадратное уравнение - условие A=default
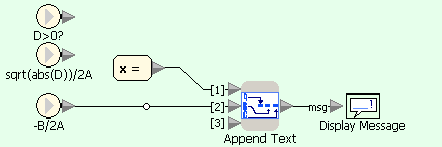
Квадратное уравнение - условие D=0
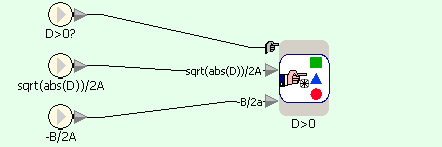
Квадратное уравнение - условие D=default (!=0)
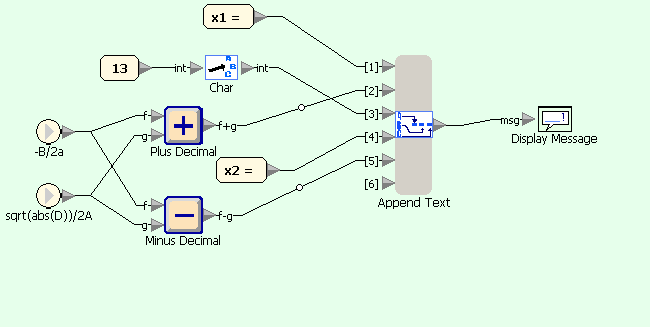
Квадратное уравнение - условие D>0
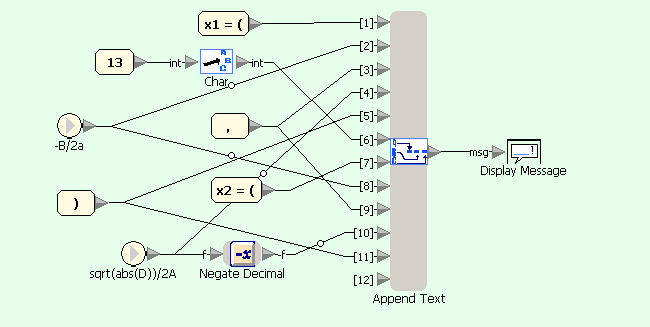
Квадратное уравнение - условие D<0
Пример для версий gc-2010-07-14
При импорте нескольких пакетов перед именем одного из них можно поставить точку, и использовать его функции без префикса имени пакета, как fmt в этом примере.
Чтобы прочитать число, введенное пользователем, следует прочитать строку из консоли, убрать последний символ переноса строки и преобразовать ее в нужный формат числа. В данном случае входные переменные будут целочисленными, но в дальнейшем будут использоваться для вычислений с плавающей точкой. Go не поддерживает неявные преобразования типов, поэтому лучше сразу трактовать входные данные как float64 (тип данных, который передается в качестве аргумента в math.Sqrt).
= — простое присваивание, := — присваивание с объявлением переменной, находящейся слева от знака присваивания. Следует отметить, что объявленные, но неиспользованные переменные считаются ошибками компиляции.
package main
import (
"os"
. "fmt"
"math"
"bufio"
"strconv")
func main() {
in := bufio.NewReader(os.Stdin)
line, err := in.ReadString('\n')
line = line[0 : len(line)-1]
A, err := strconv.Atof64(line)
if (A == 0) {
Print("Not a quadratic equation.")
return
}
line, err = in.ReadString('\n')
line = line[0 : len(line)-1]
B, err := strconv.Atof64(line)
line, err = in.ReadString('\n')
line = line[0 : len(line)-1]
C, err := strconv.Atof64(line)
if err != nil {
Print(err)
}
D := B*B-4*A*C
if (D == 0) {
Printf("x = %f", -B/2/A)
return
}
if (D>0) {
Printf("x1 = %f\nx2 = %f", -B/2/A + math.Sqrt(D)/2/A, -B/2/A - math.Sqrt(D)/2/A)
} else {
Printf("x1 = (%f, %f)\nx2 = (%f, %f)", -B/2/A, math.Sqrt(-D)/2/A, -B/2/A, -math.Sqrt(-D)/2/A)
}
}
Пример для версий Lua 5.1
*n указывает на то, что читается число.
local A = io.read('*n')
if A==0 then
io.write('Not a quadratic equation.')
return
end
local B = io.read('*n')
local C = io.read('*n')
D = B*B-4*A*C
if D==0 then
io.write('x = ', -B/2/A)
else if D>0 then
io.write('x1 = ', (-B+math.sqrt(D))/2/A, '\nx2 = ', (-B-math.sqrt(D))/2/A)
else
io.write('x1 = (', -B/2/A, ',', math.sqrt(-D)/2/A, ')\nx2 = (', -B/2/A, ',', -math.sqrt(-D)/2/A, ')\n')
end
end
Пример для версий Perl 5.12.1
В Perl 6 нет обратной совместимости, поэтому этот пример не работает в Perl 6.
$A = <>;
if ($A == 0) {
print "Not a quadratic equation.";
}
else {
$B = <>;
$C = <>;
$D = $B * $B - 4 * $A * $C;
if ($D == 0) {
print "x = ", -0.5 * $B / $A;
}
else {
if ($D > 0) {
print "x1 = ", 0.5*(-$B + sqrt($D))/$A, "\nx2 = ", 0.5*(-$B - sqrt($D))/$A
}
else {
print "x1 = (", -0.5*$B/$A, ",", 0.5*sqrt(-$D)/$A, ")\nx2 = (", -0.5*$B/$A, ",", -0.5*sqrt(-$D)/$A, ")\n"
}
}
}
Пример для версий rakudo-2010.08
Основных отличий от примера для Perl 5 два: команды чтения с консоли и вывода на печать и то, что все переменные должны быть объявлены при помощи зарезервированного слова my (объявление типа переменной остается опциональным).
my $A = $*IN.get;
if ($A == 0) {
say "Not a quadratic equation.";
}
else {
my $B = $*IN.get;
my $C = $*IN.get;
my $D = $B * $B - 4 * $A * $C;
if ($D == 0) {
say "x = ", -0.5 * $B / $A;
}
else {
if ($D > 0) {
say "x1 = ", 0.5*(-$B + sqrt($D))/$A, "\nx2 = ", 0.5*(-$B - sqrt($D))/$A
}
else {
say "x1 = (", -0.5*$B/$A, ",", 0.5*sqrt(-$D)/$A, ")\nx2 = (", -0.5*$B/$A, ",", -0.5*sqrt(-$D)/$A, ")\n"
}
}
}
Пример для версий B-Prolog 7.4-3, gprolog 1.3.0, swipl 5.6.x
Этот пример соответствует стандарту ISO Prolog и использует встроенный предикат read/1. Следует отметить, что при вводе термов этим способом после каждого терма следует ставить точку.
q :- write('A = '),
read(A),
( A = 0, write('Not a quadratic equation');
write('B = '),
read(B),
write('C = '),
read(C),
D is B*B-4*A*C,
( D = 0, write('x = '), X is -B/2/A, write(X);
D > 0, write('x1 = '), X1 is (-B+sqrt(D))/2/A, write(X1), nl, write('x2 = '), X2 is (-B-sqrt(D))/2/A, write(X2);
R is -B/2/A, I is abs(sqrt(-D)/2/A),
write('x1 = ('), write(R), write(', '), write(I), write(')'), nl,
write('x1 = ('), write(R), write(', -'), write(I), write(')')
)
).
Пример для версий gprolog 1.3.0
read_integer — не стандартный предикат, а расширение GNU Prolog, поэтому этот пример не будет работать в других реализациях.
q :- write('A = '),
read_integer(A),
( A = 0, write('Not a quadratic equation');
write('B = '),
read_integer(B),
write('C = '),
read_integer(C),
D is B*B-4*A*C,
( D = 0, write('x = '), X is -B/2/A, write(X);
D > 0, write('x1 = '), X1 is (-B+sqrt(D))/2/A, write(X1), nl, write('x2 = '), X2 is (-B-sqrt(D))/2/A, write(X2);
R is -B/2/A, I is abs(sqrt(-D)/2/A),
write('x1 = ('), write(R), write(', '), write(I), write(')'), nl,
write('x1 = ('), write(R), write(', -'), write(I), write(')')
)
).
Пример для версий Python 2.6.5
import math
import sys
A = float(raw_input("A = "))
if A == 0:
print "Not a quadratic equation"
sys.exit()
B = float(raw_input("B = "))
C = float(raw_input("C = "))
D = B * B - 4 * A * C
if D == 0:
print "x =", -B / 2.0 / A
sys.exit()
if D > 0:
print "x1 =", (-B + math.sqrt(D)) / 2.0 / A
print "x2 =", (-B - math.sqrt(D)) / 2.0 / A
else:
print "x1 = (", -B / 2.0 / A, ",", math.sqrt(-D) / 2.0 / A, ")"
print "x2 = (", -B / 2.0 / A, ",", -math.sqrt(-D) / 2.0 / A, ")"
Пример для версий PHP 5.3.2
<?php
echo "A = ";
$A = (float) fgets(STDIN);
if ($A == 0) {
die("Not a quadratic equation\n");
}
echo "B = ";
$B = (float) fgets(STDIN);
echo "C = ";
$C = (float) fgets(STDIN);
$D = $B * $B - 4 * $A * $C;
if ($D == 0) {
echo "x = ", -$B / 2.0 / $A, "\n";
die();
}
if ($D > 0) {
echo "x1 = ", (-$B + sqrt($D)) / 2.0 / $A, "\n";
echo "x2 = ", (-$B - sqrt($D)) / 2.0 / $A, "\n";
} else {
echo "x1 = (", -$B / 2.0 / $A, ", ", sqrt(-$D) / 2.0 / $A, ")\n";
echo "x2 = (", -$B / 2.0 / $A, ", ", -sqrt(-$D) / 2.0 / $A, ")\n";
}
?>
Пример для версий Mozart 1.4.0
Oz — строго типизированный язык, поэтому все преобразования между строковыми и числовыми типами выполняются в явном виде. Коэффициенты преобразуются вначале в целые числа, а потом в числа с плавающей точкой, потому что при попытке преобразовать строку “1” сразу в число с плавающей точкой возникает ошибка (строка “1.” преобразуется нормально). Унарный минус в Oz обозначается ~.
functor
import
Application System Open
define
local
A B C D
class TextFile from Open.file Open.text end
StdIn = {New TextFile init(name:stdin)}
in
{System.showInfo "A = "}
A = {Int.toFloat {String.toInt {StdIn getS($)}}}
if A==0 then
{System.showInfo "Not a quadratic equation."}
{Application.exit 0}
end
{System.showInfo "B = "}
B = {Int.toFloat {String.toInt {StdIn getS($)}}}
{System.showInfo "C = "}
C = {Int.toFloat {String.toInt {StdIn getS($)}}}
D = B*B - 4.0*A*C
if D==0.0 then
{System.showInfo "x = "#{Float.toString ~0.5*B/A}}
{Application.exit 0}
end
if D>0.0 then
{System.showInfo "x1 = "#{Float.toString ~0.5*(B-{Sqrt D})/A}}
{System.showInfo "x2 = "#{Float.toString ~0.5*(B+{Sqrt D})/A}}
else
{System.showInfo "x1 = ("#{Float.toString ~0.5*B/A}#","#{Float.toString 0.5*{Sqrt ~D}/A}#")"}
{System.showInfo "x2 = ("#{Float.toString ~0.5*B/A}#","#{Float.toString ~0.5*{Sqrt ~D}/A}#")"}
end
{Application.exit 0}
end
end
Пример для версий ActiveTcl 8.5, JTcl 2.1.0, Tcl 8.4, Tcl 8.5.7
set A [gets stdin]
if {$A==0} {
puts "Not a quadratic equation.";
return
}
set B [gets stdin]
set C [gets stdin]
set D [expr {$B*$B-4*$A*$C}]
set r [expr {-0.5*$B/$A}]
set i [expr {0.5*sqrt(abs($D))/$A}]
if {$D==0} {
puts "x = $r"
} elseif {$D>0} {
puts "x1 = [expr {$r+$i}]"
puts "x2 = [expr {$r-$i}]"
} else {
puts "x1 = ($r, $i)"
puts "x2 = ($r, [expr {-$i}])"
}
Пример для версий Bash 4.0.35, Bash 4.1.5
Сам по себе Bash не работает с числами с плавающей точкой, поэтому для вычисления корней приходится обращаться к bc.
read A;
if [ $A = 0 ]; then
echo "Not a quadratic equation.";
exit 0;
fi
read B;
read C;
D=$(( ($B)*($B)-4*($A)*($C) ));
#integer math only!
if [ $D = 0 ]; then
echo -n "x = "
echo -e "scale=3\n-0.5*($B)/($A)" | bc
exit 0;
fi
echo $D
if [ $D -gt 0 ]; then
echo -n "x1 = "
echo -e "scale=3\n0.5*(-($B)+sqrt($D))/($A)" | bc
echo -n "x2 = "
echo -e "scale=3\n0.5*(-($B)-sqrt($D))/($A)" | bc
else
echo -n "x1 = ("
echo -e "scale=3\n-0.5*($B)/($A)" | bc
echo -n ", "
echo -e "scale=3\n0.5*sqrt(-($D))/($A)" | bc
echo ")"
echo -n "x2 = ("
echo -e "scale=3\n-0.5*($B)/($A)" | bc
echo -n ", "
echo -e "scale=3\n-0.5*sqrt(-($D))/($A)" | bc
echo ")"
fi
Пример для версий boo 0.8.2
A = int.Parse(prompt("A = "))
if A==0 :
print "Not a quadratic equation."
return
B = int.Parse(prompt("B = "))
C = int.Parse(prompt("C = "))
D = B*B-4*A*C
if D==0 :
x = -0.5*B/A
print "x = ${x}"
return
if D>0 :
x1 = 0.5*(-B-System.Math.Sqrt(D))/A
x2 = 0.5*(-B+System.Math.Sqrt(D))/A
print "x1 = ${x1}"
print "x2 = ${x2}"
else :
r = -0.5*B/A
i = 0.5*System.Math.Sqrt(-D)/System.Math.Abs(A)
print "x1 = (${r},${i})"
print "x2 = (${r},-${i})"
Пример для версий Ruby 1.9.2
puts 'A = '
A = gets.chomp.to_f
if (A == 0)
puts 'Not a quadratic equation.'
return
end
puts 'B = '
B = gets.chomp.to_f
puts 'C = '
C = gets.chomp.to_f
D = B*B - 4*A*C
if (D == 0)
puts 'x = '+(-B/2/A).to_s
else
if (D > 0)
puts 'x1 = '+((-B-Math.sqrt(D))/2/A).to_s
puts 'x2 = '+((-B+Math.sqrt(D))/2/A).to_s
else
puts 'x1 = ('+(-B/2/A).to_s+','+(Math.sqrt(-D)/2/A).to_s+')'
puts 'x2 = ('+(-B/2/A).to_s+','+(-Math.sqrt(-D)/2/A).to_s+')'
end
end
Пример для версий Web2c 2009
Данный пример использует TeX-пакет для арифметики с фиксированный запятой fp и макрос этого пакета для решения квадратных уравнений \FPqsolve. Данный макрос может находить только вещественные корни уравнения, и завершается с ошибкой “FP error: Quadratic equation does not have a solution” если корни комплексные (т.е. вещественных корней нет).
\input fp.tex
\message{A = }
\read -1 to \a
\message{B = }
\read -1 to \b
\message{C = }
\read -1 to \c
\FPqsolve{\xone}{\xtwo}{\number\a}{\number\b}{\number\c}
$\a x^2+\b x+\c=0$
$x_1=\xone$
$x_2=\xtwo$
\bye
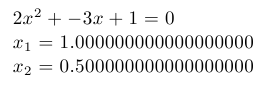
Квадратное уравнение: документ, сгенерированный TeX-программой
Пример для версий Baltie 3
Для вывода разных корней уравнения в разных строках используется перемещение спрайта. В примере показано использование конструкции “если … то … иначе …”.
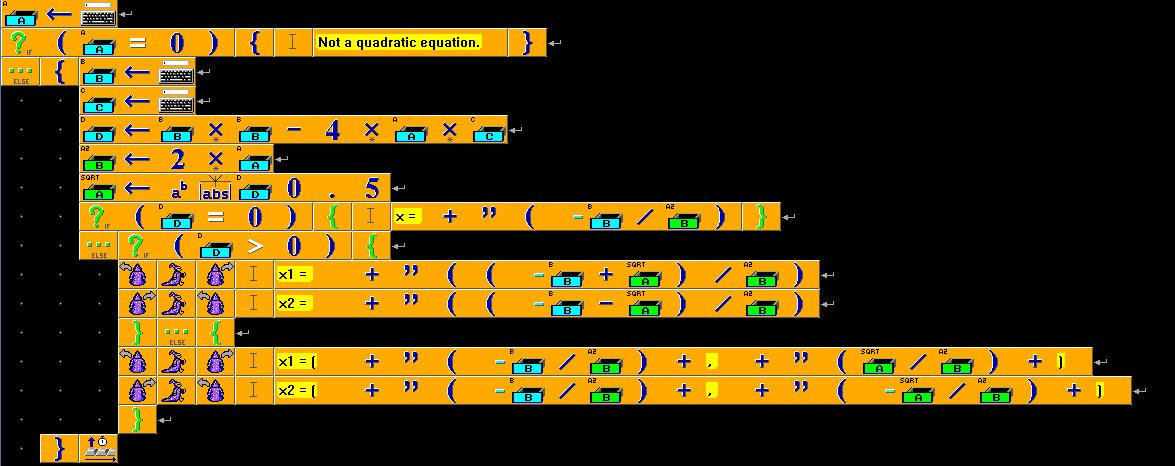
Квадратное уравнение на Baltie 3
Пример для версий Io-2008-01-07
Для вывода строки, состоящей из нескольких элементов, используется следующий прием: из этих элементов создается список (команда list), затем он конкатенируется в одну строку (join), которая и выводится на печать.
A := File standardInput readLine asNumber;
if(A==0,
"Not a quadratic equation." println;
return;
);
B := File standardInput readLine asNumber;
C := File standardInput readLine asNumber;
D := B*B-4*A*C;
A2 := 2*A;
if(D==0,
list("x = ", (-B/A2) asString) println;
return;
);
sqrtD := D abs sqrt;
if(D>0,
list("x1 = ", ((-B+sqrtD)/A2) asString) join println;
list("x2 = ", ((-B-sqrtD)/A2) asString) join println,
list("x1 = (", (-B/A2) asString, ", ", (sqrtD/A2) asString, ")") join println;
list("x2 = (", (-B/A2) asString, ", ", (-sqrtD/A2) asString, ")") join println;
);
Пример для версий iconc 9.4
procedure main ()
A := read();
if A = 0 then {
write("Not a quadratic equation.");
return;
}
B := read();
C := read();
D := B*B - 4*A*C;
if D = 0 then {
write("x = ", -B/2/A);
return;
}
if D > 0 then {
write("x1 = ", (-B+sqrt(D))/2/A);
write("x2 = ", (-B-sqrt(D))/2/A);
} else {
write("x1 = (", -B/2/A, ",", sqrt(-D)/2/A, ")");
write("x2 = (", -B/2/A, ",", -sqrt(-D)/2/A, ")");
}
end
Пример для версий gst 3.1
a := (stdin nextLine) asNumber.
(a == 0)
ifTrue: [
'Not a quadratic equation.' displayNl.
]
ifFalse: [
b := (stdin nextLine) asNumber.
c := (stdin nextLine) asNumber.
d := (b * b) - (4 * a * c).
(d == 0)
ifTrue: [
'x = ' display.
((-1)*b/2/a) displayNl.
]
ifFalse: [
(d > 0)
ifTrue: [
'x1 = ' display.
((-1)*b+(d sqrt)/2/a) displayNl.
'x2 = ' display.
((-1)*b-(d sqrt)/2/a) displayNl.
]
ifFalse: [
'x1 = (' display.
((-1)*b/2/a) display.
',' display.
((d abs sqrt)/2/a) display.
')' displayNl.
'x2 = (' display.
((-1)*b/2/a) display.
',' display.
((-1)*(d abs sqrt)/2/a) display.
')' displayNl.
].
].
].
Пример для версий Clojure 1.0.0, Clojure 1.1.0
(defn solve-quadratic [a b c]
(if (= a 0)
"Not a quadratic equation."
(let [D (- (* b b) (* 4 a c))
k1 (- 0 b)
k2 (* 2 a)]
(if (= D 0)
(str "x = " (/ k1 k2))
(if (> D 0)
(let [k3 (Math/sqrt D)]
(str (str "x1 = " (/ (+ k1 k3) k2) (str "\nx2 = " (/ (- k1 k3) k2)))))
(let [k3 (/ (Math/sqrt (- 0 D)) k2)]
(str (str (str (str "x1 = (" (/ k1 k2)) (str ", " k3)) ")\nx2 = (") (str (str (/ k1 k2) ", ") (str (- 0 k3) ")") ))
))))))
(import '(java.util Scanner))
(def scan (Scanner. *in*))
(def a (.nextInt scan))
(def b (.nextInt scan))
(def c (.nextInt scan))
(println (solve-quadratic a b c))
Пример для версий Pike 7.6, Pike 7.8
int main() {
int A = (int)Stdio.stdin->gets();
if (A == 0) {
write("Not a quadratic equation.\n");
return 0;
}
int B = (int)Stdio.stdin->gets();
int C = (int)Stdio.stdin->gets();
int D = (B*B-4*A*C);
write(D+"\n");
if (D == 0)
write(sprintf("x = %f\n",-B/2.0/A));
else if (D > 0) {
write(sprintf("x1 = %f\n", (-B+sqrt(D))/2.0/A));
write(sprintf("x2 = %f\n", (-B-sqrt(D))/2.0/A));
}
else {
write(sprintf("x1 = (%f, %f)\n", -B/2.0/A, sqrt(-D)/2.0/A));
write(sprintf("x1 = (%f, %f)\n", -B/2.0/A, -sqrt(-D)/2.0/A));
}
return 0;
}
Пример для версий Objeck 2.0.3
use IO;
bundle Default {
class Quadratic {
function : Main(args : String[]) ~ Nil {
A := Console->ReadString()->ToInt();
if (A=0) {
"Not a quadratic equation."->PrintLine();
return;
};
B := Console->ReadString()->ToInt();
C := Console->ReadString()->ToInt();
D := 1.0*(B*B-4*A*C);
if (D=0) {
"x = "->Print();
(0-B/2.0/A)->PrintLine();
};
if (D>0) {
"x1 = "->Print();
((0-B+(D->SquareRoot()))/2.0/A)->PrintLine();
"x2 = "->Print();
((0-B-(D->SquareRoot()))/2.0/A)->PrintLine();
};
if (D<0) {
out := "x1 = (";
out->Append(0-B/2.0/A);
out->Append(",");
out->Append(((D->Abs())->SquareRoot())/2/A);
out->Append(")");
out->PrintLine();
out := "x2 = (";
out->Append(0-B/2.0/A);
out->Append(",");
out->Append(0-((D->Abs())->SquareRoot())/2/A);
out->Append(")");
out->PrintLine();
};
}
}
}
Пример для версий GNU Octave 3.2.3
За счет того, что Octave предназначен для работы с математическими задачами, в нем есть ряд встроенных численных методов решения стандартных задач, в том числе и нахождения корней полиномов. Чтобы найти корень полинома, достаточно вызвать функцию roots для вектора-строки, составленного из коэффициентов полинома в порядке убывания степени (т.е. коэффициент при максимальной степени x идет первым).
roots([2 -3 1])
Пример для версий gcc 4.4.3
Этот пример использует тип данных complex, впервые появившийся в C99, и функции для работы с ним.
#include <stdio.h>
#include <complex.h>
#include <math.h>
void print(int ind, double complex x) {
printf("x%d = ", ind);
if (fabs(cimag(x)) < 1e-6)
printf("%f\n", creal(x));
else printf("(%f, %f)\n", creal(x), cimag(x));
}
int main() {
double A, B, C;
double D;
printf("A = ");
scanf("%lf", &A);
if (fabs(A)<1E-3) {
printf("Not a quadratic equation\n");
return 1;
}
printf("B = ");
scanf("%lf", &B);
printf("C = ");
scanf("%lf", &C);
A *= 2;
D = B*B-A*C*2.0;
if (fabs(D)<1E-3)
printf("x = %f", creal(-B/A));
else {
print(1, (-B+csqrt(D))/A);
print(2, (-B-csqrt(D))/A);
}
return 0;
}
Пример для версий Seed7 2012-01-01
$ include "seed7_05.s7i";
include "float.s7i";
include "math.s7i";
const proc: main is func
local
var float: a is 0.0;
var float: b is 0.0;
var float: c is 0.0;
var float: d is 0.0;
begin
readln(a);
if a = 0.0 then
writeln("Not a quadratic equation.");
else
readln(b);
readln(c);
d := b ** 2 - 4.0 * a * c;
if d = 0.0 then
writeln("x = " <& (-b / 2.0 / a));
else
if d > 0.0 then
writeln("x1 = " <& ((-b + sqrt(d)) / 2.0 / a));
writeln("x2 = " <& ((-b - sqrt(d)) / 2.0 / a));
else
writeln("x1 = (" <& (-b / 2.0 / a) <& "," <& (sqrt(-d) / 2.0 / a) <& ")");
writeln("x2 = (" <& (-b / 2.0 / a) <& "," <& (-sqrt(-d) / 2.0 / a) <& ")");
end if;
end if;
end if;
end func;
Пример для версий Falcon 0.9.6.6
a = int(input())
if a == 0
printl("Not a quadratic equation.")
exit()
end
b = int(input())
c = int(input())
d = b ** 2 - 4 * a * c
if d == 0
printl("x = " + (-b / 2.0 / a))
else
if d > 0
printl("x1 = " + ((-b + d**0.5) / 2.0 / a))
printl("x2 = " + ((-b - d**0.5) / 2.0 / a))
else
printl("x1 = (" + (-b / 2.0 / a) + "," + ((-d)**0.5 / 2.0 / a) + ")")
printl("x2 = (" + (-b / 2.0 / a) + "," + (- ((-d)**0.5 / 2.0 / a)) + ")")
end
end
Пример для версий Factor 0.94
Слово quadratic-equation принимает на вход коэффициенты квадратного уравнения и выводит результаты его решения на печать, ничего не возвращая. Обратим внимание на то, что это слово определено не через токен :, как обычные слова, а через :: — это означает, что в нем будут использоваться именованные переменные с лексической областью видимости, в данном случае именованные параметры a, b и c и локальные переменные d, x0 и sd (определенные оператором :>). Такие переменные можно загружать на стек по их имени. Слова для работы с именованными переменными доступны в словаре locals.
В Factor есть встроенный тип данных для комплексных чисел; если дискриминант отрицателен, корень из него sd автоматически примет тип complex. В этом случае для вывода корней на печать используются слова real-part и imaginary-part, извлекающие действительную и мнимую части комплексного числа, соответственно.
readln читает строку из потока ввода, а string>number (словарь math.parser) преобразует строку в действительное число.
USING: formatting io kernel locals math math.functions math.parser ;
IN: quadratic-example
:: quadratic-equation ( a b c -- )
a 0 =
[ "Not a quadratic equation." printf ]
[ b sq a c * 4 * - :> d
b neg a 2 * / :> x0
d sqrt a 2 * / :> sd
d 0 =
[ x0 "x = %f\n" printf ]
[ d 0 >
[ x0 sd + x0 sd - "x1 = %f\nx2 = %f\n" printf ]
[ x0 sd + [ real-part ] [ imaginary-part ] bi "x1 = (%f, %f)\n" printf
x0 sd - [ real-part ] [ imaginary-part ] bi "x2 = (%f, %f)\n" printf ]
if
]
if
]
if ;
readln string>number
readln string>number
readln string>number
quadratic-equation
Пример для версий Oracle 11g SQL
declare
A number := '&A';
B number := '&B';
C number := '&C';
D number := B * B - 4 * A * C;
begin
if A = 0 then
dbms_output.put_line('Not a quadratic equation.');
return;
end if;
if D = 0 then
dbms_output.put_line('x = ' || to_char(-B/2/A));
elsif D > 0 then
dbms_output.put_line('x1 = ' || to_char((-B-sqrt(D))/2/A));
dbms_output.put_line('x2 = ' || to_char((-B+sqrt(D))/2/A));
else
dbms_output.put_line('x1 = (' || to_char(-B/2/A) || ', ' || to_char(sqrt(-D)/2/A) || ')');
dbms_output.put_line('x2 = (' || to_char(-B/2/A) || ', ' || to_char(-sqrt(-D)/2/A) || ')');
end if;
end;
Пример для версий loljs 1.1
HAI
HOW DUZ I SQRT X
I HAS A X_N ITZ 10
I HAS A LIMIT ITZ 100
I HAS A COUNTER ITZ 0
IM IN YR LOOP UPPIN YR COUNTER WILE COUNTER SMALLR THAN LIMIT
I HAS A TERM ITZ QUOSHUNT OF X AN X_N
TERM R SUM OF X_N AN TERM
TERM R QUOSHUNT OF TERM AN 2
X_N R TERM
IM OUTTA YR LOOP
FOUND YR X_N
IF U SAY SO
I HAS A AC
GIMMEH AC
AC IS NOW A NUMBR
BOTH SAEM AC AN 0, O RLY?
YA RLY
VISIBLE "Not a quadratic equation."
NO WAI
I HAS A BC
GIMMEH BC
BC IS NOW A NUMBR
I HAS A CC
GIMMEH CC
CC IS NOW A NUMBR
I HAS A D ITZ DIFF OF PRODUKT OF BC AN BC AN PRODUKT OF 4 AN PRODUKT OF AC AN CC
BOTH SAEM D AN 0, O RLY?
YA RLY
VISIBLE SMOOSH "x = " QUOSHUNT OF BC AN PRODUKT OF -2 AN AC
NO WAI
BOTH SAEM 0 AN SMALLR OF 0 AN D, O RLY?
YA RLY
VISIBLE SMOOSH "x1 = " QUOSHUNT OF SUM OF BC AN SQRT D AN PRODUKT OF -2 AN AC
VISIBLE SMOOSH "x2 = " QUOSHUNT OF DIFF OF BC AN SQRT D AN PRODUKT OF -2 AN AC
NO WAI
D R PRODUKT OF D AN -1
VISIBLE SMOOSH "x1 = (" QUOSHUNT OF BC AN PRODUKT OF -2 AN AC ", " QUOSHUNT OF SQRT D AN PRODUKT OF -2 AN AC ")"
VISIBLE SMOOSH "x2 = (" QUOSHUNT OF BC AN PRODUKT OF -2 AN AC ", " QUOSHUNT OF SQRT D AN PRODUKT OF 2 AN AC ")"
OIC
OIC
OIC
KTHXBYE
Пример для версий Dyalog APL 13.1
В этом примере определяется именованная D-функция, которая принимает коэффициенты уравнения как один параметр — массив из трех элементов и выводит решение уравнения. Вначале параметр разбирается на отдельные коэффициенты, и им присваиваются имена (N⊃⍵ выбирает N-ый элемент массива). Затем выполняются проверки первого коэффициента и дискриминанта, по которым функция может вернуть нетипичное решение. Наконец, оба случая ненулевого дискриминанта обрабатываются одним и тем же кодом благодаря тому, что в APL есть встроенные комплексные числа. Например, вызов функции
solve 1 0 2
возвращает следующие значения:
0J1.4142135623730951 0J¯1.4142135623730951
(J — разделитель действительной и мнимой частей числа, ¯ — “высокий” минус, использующийся для ввода/вывода отрицательных чисел).
Отметим, что данный код является нетипичным для APL из-за использования условного ветвления, а также из-за того, что механизм использования аргумента ограничивает диапазон его возможных значений до одномерного массива из трех элементов.
solve←{A←0⊃⍵ ⋄ B←1⊃⍵ ⋄ C←2⊃⍵ ⋄ A=0:'Not a quadratic equation.' ⋄ D←(B*2)-4×A×C ⋄ D=0:-0.5×B÷A ⋄ ((-B-D*0.5), -B+D*0.5)×0.5÷A}
Пример для версий Nimrod 0.8.8
from math import sqrt
from strutils import parseFloat
var A = parseFloat(readLine(stdin))
if A == 0.0:
echo "Not a quadratic equation."
else:
var B = parseFloat(readLine(stdin))
var C = parseFloat(readLine(stdin))
var D = B * B - 4.0 * A * C
if D == 0.0:
echo "x = ", -0.5 * B / A
elif D > 0.0:
echo "x1 = ", -0.5 * (B - sqrt(D)) / A
echo "x2 = ", -0.5 * (B + sqrt(D)) / A
else:
echo "x1 = (", -0.5 * B / A, ", ", 0.5 * sqrt(-D) / A, ")"
echo "x2 = (", -0.5 * B / A, ", ", -0.5 * sqrt(-D) / A, ")"
Пример для версий VBScript 5.7, VBScript 5.8
Function GetInt()
Input = WScript.StdIn.ReadLine
If not IsNumeric(Input) Then
WScript.Echo "Coefficient is not a number."
WScript.Quit
End If
GetInt = CInt(Input)
End Function
A = GetInt()
If A = 0 Then
WScript.Echo "Not a quadratic equation."
WScript.Quit
End If
B = GetInt()
C = GetInt()
D = B * B - 4 * A * C
p1 = -B / 2.0 / A
p2 = Sqr(Abs(D)) / 2.0 / A
If D = 0 Then
WScript.Echo "x = " & p1
Else
If D > 0 Then
WScript.Echo "x1 = " & (p1 + p2)
WScript.Echo "x2 = " & (p1 - p2)
Else
WScript.Echo "x1 = (" & p1 & ", " & p2 & ")"
WScript.Echo "x2 = (" & p1 & ", " & -p2 & ")"
End If
End If
Пример для версий VBA 6.3, VBA 6.5
Function GetInt(Name As String) As Integer
Dim Coef As String
Coef = Application.InputBox("Enter Coefficient " & Name)
GetInt = CInt(Coef)
End Function
Sub Quadratic()
Dim A As Integer, B As Integer, C As Integer, D As Integer
A = GetInt("A")
If A = 0 Then
MsgBox ("Not a quadratic equation.")
Exit Sub
End If
B = GetInt("B")
C = GetInt("C")
D = B * B - 4 * A * C
Dim p1 As Double, p2 As Double
p1 = -B / 2# / A
p2 = Sqr(Abs(D)) / 2# / A
If D = 0 Then
MsgBox ("x = " & CStr(p1))
Else
If D > 0 Then
MsgBox ("x1 = " & CStr(p1 + p2) & Chr(10) & "x2 = " & CStr(p1 - p2))
Else
MsgBox ("x1 = (" & CStr(p1) & ", " & CStr(p2) & ")" & Chr(10) & "x2 = (" & CStr(p1) & ", " & CStr(-p2) & ")")
End If
End If
End Sub
Пример для версий guile 1.8.5
Конструкция begin используется для того, чтобы выполнить несколько команд подряд.
(define A (read))
(define B (read))
(define C (read))
(define D (- (* B B) (* 4 A C)))
(if (= A 0)
(display "Not a quadratic equation.")
(begin
(define k1 (/ B -2 A))
(define k2 (/ (sqrt (abs D)) 2 A))
(if (= D 0)
(begin (display "x = ") (display k1))
(if (> D 0)
(begin (display "x1 = ") (display (+ k1 k2)) (newline) (display "x2 = ") (display (- k1 k2)))
(begin (display "x1 = (") (display k1) (display ", ") (display k2) (display ")") (newline)
(display "x2 = (") (display k1) (display ", ") (display (- k2)) (display ")"))))))
Пример для версий g95 0.93, gfortran 4.5.0
В примере используется встроенный тип данных complex. // — оператор конкатенации строк. Число перед скобками в описании формата означает количество раз, которые повторяется формат в скобках (в данном случае дважды — для первого и второго корней).
program Quadratic
integer :: a, b, c
real :: d, p1, p2
complex :: cp2
read (*, *), a
if (a == 0) then
write (*, *) "Not a quadratic equation"
stop
end if
read (*, *) b
read (*, *) c
d = b * b - 4 * a * c
p1 = - b / 2.0 / a
if (abs(d) < 1.0e-9) then
write (*, "(A, F8.3)") "x = ", p1
elseif (d > 0) then
p2 = sqrt(d) / 2.0 / a
write (*, "(2(A, F8.3))") "x1 = ", p1 + p2, char(13) // char(10) // "x2 = ", p1 - p2
else
cp2 = sqrt(cmplx(d)) / 2.0 / a
write (*, "(2(A, F8.3, F8.3), A)") "x1 = (", p1 + cp2, ")" // char(13) // char(10) // "x2 = (", p1 - cp2, ")"
end if
end
Пример для версий R 2.10.1
Основной средой работы с R является интерактивный интерпретатор, поэтому достаточно определить функцию, решающую уравнение, и вызывать ее с нужными коэффициентами. Используется встроенный тип complex.
quadratic <- function(a, b, c) {
if (a == 0) {
print("Not a quadratic equation.")
} else {
d <- b * b - 4 * a * c
if (d == 0) {
print(paste("x =", -b / 2 / a))
} else
if (d > 0) {
print(paste("x =", (-b + sqrt(d) * c(1, -1)) / 2 / a))
} else {
print(paste("x =", (-b + sqrt(as.complex(d)) * c(1, -1)) / 2 / a))
}
}
}
Пример для версий Dart 1.1.1
import 'dart:io';
import 'dart:math' show sqrt;
int readInt() {
String input = stdin.readLineSync();
return int.parse(input);
}
main() {
int A, B, C;
try {
A = readInt();
B = readInt();
C = readInt();
}
on FormatException {
print("Coefficient is not a number.");
return;
}
if (A == 0) {
print("Not a quadratic equation.");
return;
}
int D = B * B - 4 * A * C;
double p1 = - B / 2.0 / A;
double p2 = sqrt(D.abs()) / 2.0 / A;
if (D == 0) {
print("x = $p1");
} else {
if (D > 0) {
print("x1 = ${p1 + p2}");
print("x2 = ${p1 - p2}");
} else {
print("x1 = ($p1, $p2)");
print("x2 = ($p1, ${-p2})");
}
}
}
Пример для версий Snap! 4.0
Одна из удобных возможностей Snap! — блок join позволяет конкатенировать произвольное количество аргументов в одном блоке.
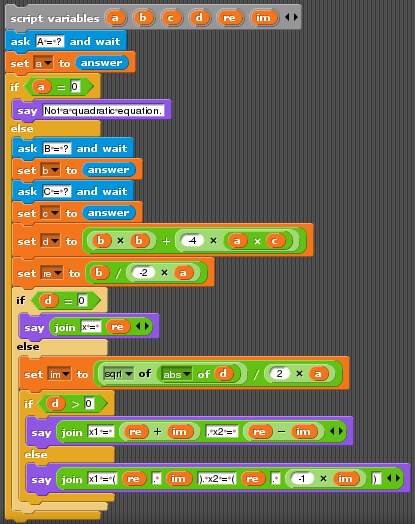
Квадратное уравнение на Snap!
Пример для версий Clarion C7
минималистическая версия
PROGRAM
OMIT('***')
* User: Shur
* Date: 28.02.2016
* Time: 14:05
***
MAP
END
A REAL
B REAL
C REAL
root CSTRING(64)
CODE
A=0; B=2; C=3
!A=1; B=-5; C=3
!A=1; B=2; C=1
D$ = B * B - 4 * A * C
if A = 0
root = 'Not a quadratic equation.'
elsif D$ = 0
root = 'x = ' & -B/2/A
elsif D$ > 0 then
root = 'x1 = ' & (-B-sqrt(D$))/2/A & '|' & |
'x2 = ' & (-B+sqrt(D$))/2/A
else
root = 'x1 = (' & -B/2/A & ', ' & sqrt(-D$)/2/A & ')' & '|' & |
'x2 = (' & -B/2/A & ', ' & -sqrt(-D$)/2/A & ')'
end
message(choose(A=0,'','D='&D$&'|----------|')&root,'Quadratic equation')
Пример для версий Clarion C7
максималистичная версия с проверкой найденных корней. попутно реализована арифметика комплексных чисел
PROGRAM
OMIT('***')
* User: Shur
* Date: 28.02.2016
* Time: 14:05
***
complex GROUP,TYPE
a REAL(0)
b REAL(0)
END
MAP
cxSum PROCEDURE(*complex cxA, *complex cxB, *complex cxRes)
cxMul PROCEDURE(*complex cxA, *complex cxB, *complex cxRes)
cxDiv PROCEDURE(*complex cxA, *complex cxB, *complex cxRes)
END
A REAL
B REAL
C REAL
X GROUP,PRE(X),DIM(2)
X LIKE(complex)
F CSTRING(64)
R LIKE(complex)
END
root CSTRING(64)
check_ CSTRING(256)
CX1 LIKE(complex)
CX2 LIKE(complex)
CX3 LIKE(complex)
CODE
A=1; B=3; C=3
!A=1; B=-5; C=3
!A=1; B=2; C=1
D$ = B * B - 4 * A * C
if A = 0
root = 'Not a quadratic equation.'
elsif D$ = 0
X[1].X.a = -B/2/A
root = 'x = ' & X[1].X.a
elsif D$ > 0 then
X[1].X.a = (-B-sqrt(D$))/2/A
X[2].X.a = (-B+sqrt(D$))/2/A
root = 'x1 = ' & X[1].X.a & '|' & |
'x2 = ' & X[2].X.a
else
X[1].X.a = -B/2/A; X[1].X.b = sqrt(-D$)/2/A
X[2].X.a = -B/2/A; X[2].X.b = -sqrt(-D$)/2/A
root = 'x1 = (' & X[1].X.a & ', ' & X[1].X.b & ')' & '|' & |
'x2 = (' & X[2].X.a & ', ' & X[2].X.b & ')'
end
loop i# = 1 to 2
!loop j# = 1 to 2
if X[i#].X.a or X[i#].X.b
if D$ ~< 0
X[i#].F = choose(A=0,'',A&'*'&X[i#].X.a&'^2')&choose(B=0,'',choose(B>0,'+','')&B&'*'&X[i#].X.a)&choose(C=0,'',choose(C>0,'+','')&C)
X[i#].R.a = round(EVALUATE(X[i#].F),0.0000000000001)
check_ = check_ & choose(check_<>'','|','') & X[i#].F&'=' & X[i#].R.a
else
CX1.a = X[i#].X.a; CX1.b = X[i#].X.b
CX2.a = A; CX2.b = 0
cxMul(CX1, CX1, CX3) ! x^2
cxMul(CX2, CX3, CX3) ! a*x^2
X[i#].R = CX3
CX2.a = B; CX2.b = 0
cxMul(CX1, CX2, CX3) ! b*x
CX2 = X[i#].R
cxSum(CX2,CX3,CX1) ! a*x^2 + b*x
X[i#].R = CX1
CX2.a = C; CX2.b = 0
cxSum(CX1,CX2,CX3) ! a*x^2 + b*x + c
X[i#].R = CX3
check_ = check_ & choose(check_<>'','|','') &'= (' & X[i#].R.a & ', ' & X[i#].R.b & ')'
end
end
!end
end
message(choose(A=0,'','D='&D$&'|----------|')&|
root&|
choose(A=0,'',choose(check_>'',|
'|----------|'&|
check_,'')),'Quadratic equation')
cxSum PROCEDURE(cxA, cxB, cxRes)
CODE
cxRes.a = cxA.a + cxB.a
cxRes.b = cxA.b + cxB.b
cxMul PROCEDURE(cxA, cxB, cxRes)
CODE
cxRes.a = cxA.a*cxB.a - cxA.b*cxB.b
cxRes.b = cxA.a*cxB.b + cxB.a*cxA.b
cxDiv PROCEDURE(cxA, cxB, cxRes)
CODE
cxRes.a = (cxA.a*cxB.a + cxA.b*cxB.b) / (cxB.a^2 + cxB.a^2)
cxRes.b = (cxB.a*cxA.b - cxB.b*cxA.a) / (cxB.a^2 + cxB.a^2)