TeX
- Дата создания:
- 1978
- Парадигма:
- Типизация:
- Принятые расширения файлов:
- .tex
- Реализации и версии (свернуть все | развернуть все):
TeX — система набора текста и верстки, разработанная профессором Дональдом Кнутом.
Команды TeX обычно начинаются с обратной косой черты и группируются при помощи фигурных скобок. Почти все синтаксические свойства языка могут быть изменены “на лету”, что делает сложным синтаксический разбор TeX при помощи чего-либо, отличного от самого TeX. Многие команды, включая большинство определенных пользователем, разворачиваются до тех пор, пока не останутся только неразворачиваемые символы. Сама процедура развертывания практически лишена побочных эффектов. Хвостовая рекурсия оптимизируется. Присутствуют конструкции if-then-else.
Хотя TeX является системой набора и верстки, развитые возможности макроязыка TeX делают его Тьюринг-полным языком программирования.
Элементы синтаксиса:
| Комментарий до конца строки | % |
|---|---|
| Присваивание значения переменной | varname = value |
| Блок | { ... } |
Логотип TeX
Примеры:
Квадратное уравнение:
Пример для версий Web2c 2009Данный пример использует TeX-пакет для арифметики с фиксированный запятой fp и макрос этого пакета для решения квадратных уравнений \FPqsolve. Данный макрос может находить только вещественные корни уравнения, и завершается с ошибкой “FP error: Quadratic equation does not have a solution” если корни комплексные (т.е. вещественных корней нет).
\input fp.tex
\message{A = }
\read -1 to \a
\message{B = }
\read -1 to \b
\message{C = }
\read -1 to \c
\FPqsolve{\xone}{\xtwo}{\number\a}{\number\b}{\number\c}
$\a x^2+\b x+\c=0$
$x_1=\xone$
$x_2=\xtwo$
\bye
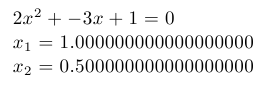
Квадратное уравнение: документ, сгенерированный TeX-программой
Факториал:
Пример для версий Web2c 2009Данный пример использует итеративное определение факториала.
В макросе \factorial используются двойные фигурные скобки, т.к. в макросе присутствует цикл, который вызывается внутри другого цикла.
Рассчитываются только факториалы чисел до 12 включительно. Для больших чисел выполнение завершается с ошибкой “Arithmetic overflow”.
\newcount\n \newcount\p \newcount\m
\def\factorial#1{{\m=#1\advance\m by 1
\n=1
\p=1
\loop\ifnum\n<\m \multiply\p by \n \advance\n by 1 \repeat\number\p}}
\def\printfactorials#1{\m=#1\advance\m by 1
\n=0
\loop\ifnum\n<\m \hfil\break\number\n! = \factorial{\n} \advance\n by 1 \repeat}
\printfactorials{12}
\bye
Числа Фибоначчи:
Пример для версий Web2c 2009Данный пример использует итеративный процесс для расчета чисел Фибоначчи.
В макросе \fibonacci используются двойные фигурные скобки, т.к. в макросе присутствует цикл, который вызывается внутри другого цикла.
\newcount\n \newcount\np \newcount\npp \newcount\m \newcount\f
\def\fibonacci#1{{\ifnum #1<3 1\else
\np=1\npp=1\m=3
\loop\ifnum\m<#1\f=\npp\npp=\np\advance\np by\f\advance\m by 1\repeat
\f=0\advance\f by\np\advance\f by\npp
\number\f\fi}}
\def\printfibonacci#1{\m=#1\advance\m by 1
\n=1
\loop\ifnum\n<\m\fibonacci{\n}, \advance\n by 1\repeat...}
\printfibonacci{16}
\bye
Hello, World!:
Пример для версий Web2c 2009Hello, World!
\bye
Комментарии
]]>blog comments powered by Disqus
]]>